O intervalo de confiança [224,8; 233,0] para a média populacional de uma variável X, normalmente distribuída, foi obtido por meio de uma amostra aleatória de tamanho 100. Para a obtenção do intervalo considerou-se a população de tamanho infinito, um nível de confiança de 90% e a informação de que na distribuição normal padrão (Z) a probabilidade P(Z > 1,64) = 0,05. A variância populacional da variável X é, no caso,
Para analisar a distribuição da renda familiar mensal de dois grupos 1 e 2, considere o desenho esquemático abaixo que apresenta a distribuição das respectivas rendas em cada grupo.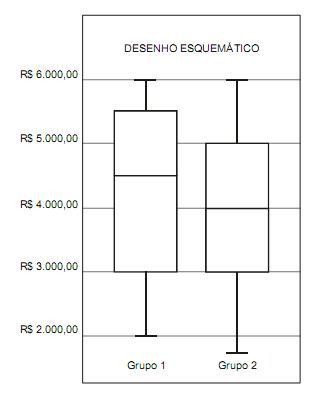 
Com relação aos diagramas dos dois grupos, verifica-se que
Em uma distribuição uniformemente distribuída sobre o intervalo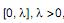 
extraiu-se uma amostra aleatória de 10 elementos, com reposição. O maior valor dos elementos desta amostra apresentou um valor igual a M. Com isto, obteve-se que o estimador de máxima verossimilhança da variância da população foi igual a 27. O estimador de máxima verossimilhança da média da população é
Uma variável aleatória U tem distribuição uniforme contínua no intervalo [a, 3a]. Sabe-se que U tem média 12. Uma amostra aleatória simples de tamanho n, com reposição, é selecionada da distribuição de U e sabe-se que a variância da média dessa amostra é 0,1. Nessas condições, o valor de n é
O peso de um saco de batatas é uma variável aleatória, X, que tem distribuição normal com média 30 kg e desvio padrão 2 kg. Um caminhão é carregado com 100 sacos. Considerando que o peso desses sacos é uma amostra aleatória simples da distribuição de X, a probabilidade da carga do caminhão pesar pelo menos 2985 kg é
A figura apresenta dois gráficos de caixa (boxplots), que foram construídos a partir de dois conjuntos de dados diferentes. O quadro apresenta algumas estatísticas descritivas para quatro conjuntos de dados. A partir da análise dos gráficos da figura e das estatísticas descritivas no quadro, é possível associar cada um dos gráficos (grupos 1 e 2) a um dos conjuntos de dados (I, II, III ou IV). Observe.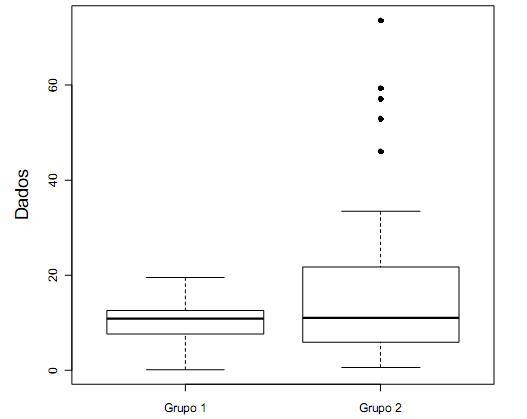
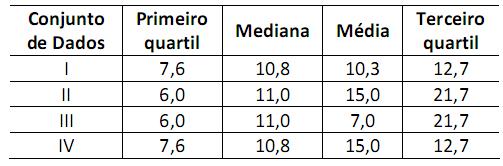
Assinale a associação correta.
Observe a tabela com classificações de variáveis e exemplos.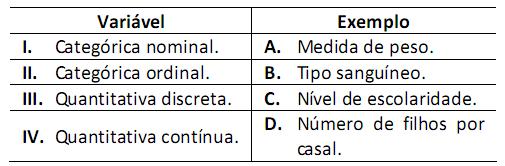 
A relação correta entre esses dois conjuntos é
As informações abaixo foram extraídas de um quadro de análise de variância, cujo objetivo é testar a hipótese da igualdade das médias da variável X de 4 grupos I, II, III e IV, independentes, cada um contendo 8 observações. 
O valor da estatística F (F calculado) utilizado para a verificação da igualdade das médias é
Sabe-se que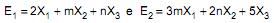 
são 2 estimadores não viesados utilizados para a média µ diferente de zero de uma população normal com variância unitária. Considere que 
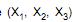é uma amostra aleatória de tamanho 3 extraída, com reposição, desta população, sendo m e n parâmetros reais. Entre os 2 estimadores, o mais eficiente apresenta uma variância igual a
Considere duas variáveis X e Y representando o peso (em kg) e a altura (em cm), respectivamente, dos 100 sócios de um clube. Em um censo realizado neste clube, foram apurados os seguintes resultados: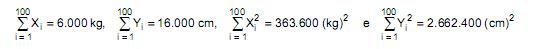 
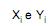são o peso e a altura, respectivamente, do i-ésimo sócio
(i = 1, 2, 3, . . . ,100).
Está correto afirmar que o coeficiente de variação de
Considere as seguintes afirmações:
I. Uma intervenção que afeta uma série temporal pode mudar o nível da série, podendo também afetar a sua variabilidade.
II. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não correlacionados.
III. Para o modelo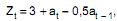 
onde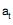 
é ruído branco de média zero e variância σ2, a previsão de origem t e horizonte 2 é igual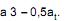 
IV. Se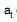 
é ruído branco de média zero e variância σ2 um modelo do tipo 
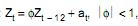, é estacionário de médias móveis sazonal.
Dentre as afirmações acima são verdadeiras APENAS
Seja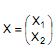 
um vetor de variáveis aleatórias e seja 
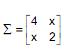sua matriz de covariâncias. Seja λ a primeira componente principal da matriz ∑ . Sabendo que a proporção da variância total de X que é explicada por λ é 
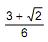o valor de x é
Sabe-se que o caixa de uma empresa segue um processo generalizado de Wiener, com variância de 400 por mês. O desvio-padrão do caixa da empresa depois de quatro meses é
O desvio-padrão amostral de X: {3; 5; 9; 11; 13; 19} é, com aproximação de duas casas decimais
