Uma empresa selecionou 160 candidatos para uma entrevista, visando o preenchimento de algumas vagas. Dos candidatos selecionados, 5% não compareceram à entrevista, e 25% dos que compareceram foram contratados. Em relação ao número inicial de candidatos selecionados, aqueles que foram contratados representam
Um anagrama de uma palavra é obtido através da alteração da ordem das letras dessa palavra, mantendo-se a mesma quantidade de letras da palavra inicial. A própria palavra inicial é considerada um dos seus anagramas e não há necessidade de que o termo formado tenha significado no nosso idioma. Por exemplo, um dos anagramas da palavra roupa é o termo apour. Dessa forma, podemos afirmar que a quantidade de anagramas da palavra mercado, iniciados por uma consoante é:
A secretaria de uma universidade possui duas impressoras capazes de imprimir juntas 50.000 cópias no período de cinco dias. Sabendo que foram adquiridas mais quatro impressoras de igual capacidade de produção, calcule quantos dias as seis impressoras juntas levarão para produzir 90.000 cópias e assinale a alternativa correta.
Pesquisas em ciências exatas geralmente utilizam softwares com grande poder de tratamento de dados. Entretanto, é necessário um conhecimento mínimo para trabalhar com eles.
Se em uma simulação de dados numéricos forem gerados os conjuntos
Duas torneiras abertas e com mesma vazão enchem um tanque, que estava vazio, em 18 horas. Se mais uma torneira, idêntica às duas, e com mesma vazão, fosse aberta, então o tanque seria completamente cheio em:
Considere que um reservatório possui o formato de um cilindro reto, cujo raio da base mede 4 cm e a altura mede 10 cm. Considere, também, um balde com o formato de um prisma, cuja base é um retângulo com comprimento e largura medindo 2 cm e 1 cm, respectivamente, e cuja altura mede 2 cm.
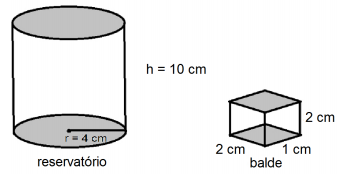
Pretende-se preencher todo o volume desse reservatório com água. Para tal, primeiramente preenche-se o volume do balde com água e, em seguida, despeja-se o conteúdo do balde no reservatório. Esse processo é repetido até que o reservatório esteja totalmente cheio. Dessa forma, a quantidade mínima de vezes que o balde deve ser preenchido com água, para que se preencha todo o volume do reservatório com essa mesma água, será igual a
(considere o valor de π = 3)
A razão entre o volume de uma esfera inscrita em cone reto de raio da base R e altura 2R e o volume do cone é
As 20 vagas de um estacionamento são organizadas em 4 fileiras de 5 vagas cada, sendo as vagas da primeira fileira numeradas de um a cinco [1 a 5], da segunda fileira de seis a dez [6 a 10] e assim sucessivamente. Quatro veículos entram no estacionamento vazio. A probabilidade de que os quatros veículos estacionem em vagas numeradas com números primos, e em fileiras distintas é
Oito crianças são dispostas em duas rodas em salas A e B, cada roda com 4 [quatro] crianças. O número de modos diferentes de dispor as 8 [oito] crianças é
Um dos valores da potência complexa é igual a
Em certo dia, em uma empresa onde trabalham 36 pessoas, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas era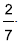 
No dia seguinte, constatou-se que mais uma dessas pessoas estava resfriada. Assim, a razão do número de pessoas resfriadas para o número de pessoas não resfriadas passou a ser
Um terreno retangular foi dividido em dois lotes, Ι e ΙΙ, conforme mostra a figura, sendo que as medidas indicadas estão em metros.
Sabendo que o lote Ι tem a forma de um quadrado com 900 m² de área, então a área total desse terreno é
Seja ABC um triângulo retângulo com vértices A = (0,0), B = (x,0) e C = (0,y), com x > 0 e y > 0. Sabendo que a reta que passa pelos vértices B e C também passa pelo ponto (4,1), temos que o comprimento L da hipotenusa de ABC é dado, em funçao de x, por
Considere o sistema cartesiano ortogonal s
1 = (0,x,y) no plano. Sejam o ponto P = (2,3) e a reta r: 2x - y +5 = 0. Seja s2 =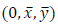 
o sistema obtido pela rotação do sistema s1 de 
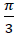radianos no sentido anti-horário. Então, a equação da reta r no sistema Seja s2 = 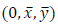é dada por
Sejam f e g funções definidas em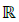 
e a, b ∈
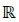. A função y = af(x) + bg(x) é chamada combinação linear de f e g se f(x) = sen(kx) e g(x) = cos (kx), em que k é uma constante real. Então, qualquer combinação linear de e pode ser escrita nas formas
