O estimador de máxima verossimilhança não viesado, por correção de Bessel, da variância de uma amostra de tamanho n=4 é igual a 3 unidades.
O valor do estimador de máxima verossimilhança da variância dessa população (na mesma unidade de medida) é:
É uma técnica que busca localizar os valores dos parâmetros que ampliam a função de verossimilhança, que mede a probabilidade dos dados pesquisados dado o modelo. Esse método é amplamente utilizado e pode ser aplicado a diversostipos de modelos, como regressão linear, modeloslineares generalizados e outros. Esse conceito refere-se a
A estimação por métodos computacionais é uma área da estatística que utiliza técnicas computacionais para estimar parâmetros desconhecidos em modelos estatísticos. Assinale a alternativa correta em relação aos métodos:

Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
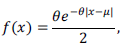
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
A estimativa de máxima verossimilhança para o parâmetro μ é igual a 10,4.
O quadro abaixo mostra a realização de uma amostra aleatória simples u1, u2, u3, u4, que foi retirada de uma distribuição uniforme contínua no intervalo [0, a].
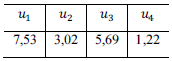
Considerando que a representa a estimativa de máxima verossimilhança do parâmetro a, julgue o item seguinte.
A estimativa de máxima verossimilhança para a média da distribuição em tela é igual a 4,365

Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
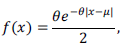
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
A estimativa de máxima verossimilhança do desvio padrão populacional é igual a em que representa a estimativa de máxima verossimilhança do parâmetro θ.
Com base nesses dados, em um grupo de 80 pessoas que vivem em comunidades rurais em média, quantas teriam acesso à internet?

Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
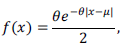
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
A estimativa de máxima verossimilhança da moda populacional é igual a 10,6.


