Com relação a estatística, julgue os itens seguintes.
Considere que, com base em um levantamento amostral, um pesquisador tenha observado que determinada medida antropométrica dos indivíduos de um grupo A é, em média, igual ao dobro dessa mesma medida em indivíduos do grupo B, e que, com base nessa observação, o pesquisador tenha concluído que essa mesma relação deve ocorrer na população. Com base nessas informações, é correto afirmar que o pesquisador não seguiu os princípios essenciais para a elaboração de inferências estatísticas, pois a simples avaliação visual (ou descritiva) da diferença entre médias de grupos pode não refletir o comportamento populacional, já que há outros aspectos relevantes para a análise, como o tamanho da amostra e a variabilidade das medidas dentro de cada grupo de indivíduos.
Sobre cadeias de Markov, analise.
I. Uma cadeia de Markov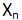 
tem probabilidades de transição homogêneas se as probabilidades de transição para um passo são fixas e não variam com o tempo.
II. O tempo de ocupação de estados para cadeias de Markov de tempo contínuo segue uma distribuição binomial no qual X(t) permanece em um determinado estado para um intervalo de tempo aleatório normalmente distribuído.
III. A função de massa de probabilidade conjunta para (k + 1) instantes de tempo arbitrários de uma cadeia de Markov é dada por: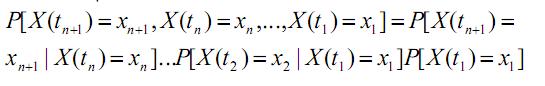 
Assinale
Sobre métodos numéricos diretos, analise.
I. A regra de Cramer exige o cálculo de n-1 determinantes.
II. O método de eliminação de Gauss consiste em transformar o sistema linear original em um sistema linear equivalente com matriz dos coeficientes triangular superior.
III. O processo de fatoração LU consiste em decompor a matriz A dos coeficientes em um produto de um ou dois fatores e, em seguida, resolver uma sequência de sistemas lineares.
Assinale
Sobre o método de Newton-Raphson é correto afirmar que
Sobre cointegração entre duas séries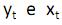 
na análise de séries temporais é INCORRETO afirmar que
Na média, o número de vezes que um dado de 6 lados deve ser jogado até que todos os lados apareçam pelo menos uma vez é
A figura apresenta dois gráficos de caixa (boxplots), que foram construídos a partir de dois conjuntos de dados diferentes. O quadro apresenta algumas estatísticas descritivas para quatro conjuntos de dados. A partir da análise dos gráficos da figura e das estatísticas descritivas no quadro, é possível associar cada um dos gráficos (grupos 1 e 2) a um dos conjuntos de dados (I, II, III ou IV). Observe.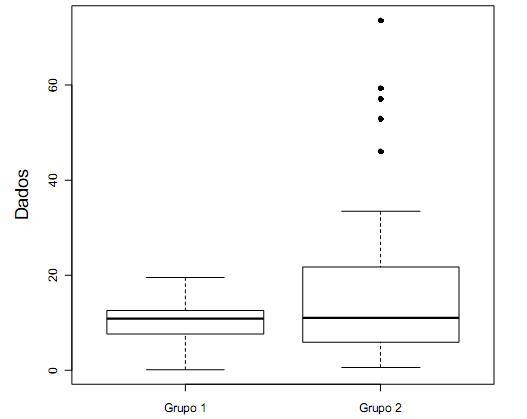
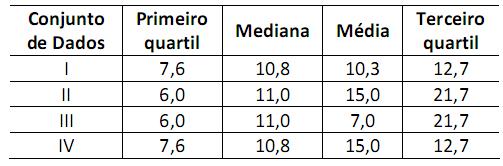
Assinale a associação correta.
Uma organização não governamental gostaria de estimar a proporção de eleitores de um estado que são contra o voto obrigatório. Uma amostra de 600 indivíduos, selecionados ao acaso dentre os eleitores do estado, foi entrevistada. Com 99% de confiança, a estimativa intervalar para a proporção de eleitores que são contrários ao voto obrigatório foi calculada, chegando-se a [0,35; 0,45]. Assinale a alternativa correta.
Em um município brasileiro, a população total no ano passado era de 10.000 habitantes, dos quais 6.000 eram do sexo feminino. Dentre as mulheres, 3.000 pertenciam à faixa etária considerada fértil (15 a 49 anos). No ano passado, foram registrados 600 nascimentos (300 dos quais eram meninas) e 100 óbitos (40 dos quais eram mulheres) no município. Considerando os dados enunciados, as taxas de fecundidade, natalidade, mortalidade e crescimento populacional relativo desse município no ano passado são, respectivamente,
Observe a tabela com classificações de variáveis e exemplos.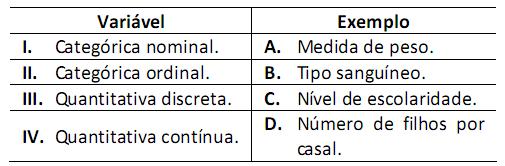 
A relação correta entre esses dois conjuntos é
Uma prefeitura comprou, para a merenda escolar, sacos de farinha de um determinado distribuidor, o qual afirma que esses sacos são normalmente distribuídos, pesando, em média, 1 Kg ou mais. Numa amostragem de 25 sacos, obteve-se uma média de 980g, com um desvio padrão de 50g. Tendo por base o valor obtido no cálculo da estatística teste e sabendo que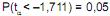 
, podemos afirmar, com 95% de confiança, que a afirmação do distribuidor é:
Com relação a estatística, julgue os itens seguintes.
Suponha que as larguras dos polegares humanos sigam uma distribuição normal com média igual a 2 cm e variância V > 0. Nesse caso, se a probabilidade de se observar um polegar com mais de 2,54 cm de largura for igual a 0,025, então V será inferior a 0,35.
As informações abaixo foram extraídas de um quadro de análise de variância, cujo objetivo é testar a hipótese da igualdade das médias da variável X de 4 grupos I, II, III e IV, independentes, cada um contendo 8 observações. 
O valor da estatística F (F calculado) utilizado para a verificação da igualdade das médias é
Sabe-se que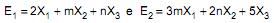 
são 2 estimadores não viesados utilizados para a média µ diferente de zero de uma população normal com variância unitária. Considere que 
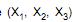é uma amostra aleatória de tamanho 3 extraída, com reposição, desta população, sendo m e n parâmetros reais. Entre os 2 estimadores, o mais eficiente apresenta uma variância igual a
Considere duas variáveis X e Y representando o peso (em kg) e a altura (em cm), respectivamente, dos 100 sócios de um clube. Em um censo realizado neste clube, foram apurados os seguintes resultados: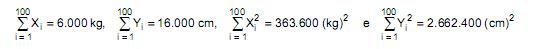 
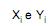são o peso e a altura, respectivamente, do i-ésimo sócio
(i = 1, 2, 3, . . . ,100).
Está correto afirmar que o coeficiente de variação de
