A tabela indica o número do calçado das crianças de uma determinada creche.
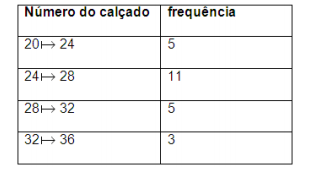
De acordo com a tabela, o terceiro quartil do número do calçado das crianças dessa creche é igual a:
De uma população foi retirada uma amostra com distribuição normal ao nível de 95%. Se o intervalo de confiança para
a variãncia é dado por: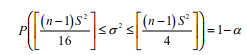
, então o intervalo de confiança para a variância populacional admitindo uma distribuição normal, n= 8. s = 4 α = 0,05 com 95 % de confiança será igual a:
A equação de regressão linear simples pelo método dos mínimos quadrados é determinada pelas seguintes
formulas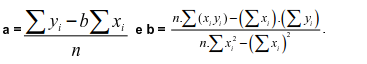
O tempo de espera de ligações em função do atendimento em um Call Center é dado pela equação de regressão
linear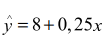
. Nessas condições, o tempo de espera de ligações em função de 15 atendimentos no Call
Center e soma de atendimentos igual a 80 é igual a:
Num lote de rodas para automóveis, sabe–se que 8 não apresentam defeitos e as 4 restantes apresentam defeitos. A probabilidade de se escolher aleatoriamente duas rodas e elas não serem defeituosas é de:
Analise a tabela a seguir.

A série acima representa as notas dos alunos na primeira avaliação de determinado curso. Em relação a esses dados, assinale a opção que apresenta os valores que representam a Média, a Mediana e a Moda, respectivamente. (considere apenas 1 casa decimal)
Analise a tabela a seguir.

As sobras de comida de um refeitório foram mediadas 30 dias sendo obtidos os dados acima em kg. Assinale a opção que apresenta a tabela que quadamente o agrupamento desses dados.
Em relação à Amostragem Aleatória Simples, é INCORRETO
afirmar que
Desejando estimar o salário médio dos gerentes de
agências bancárias, certo pesquisador tomou uma amostra
aleatória simples sem reposição de gerentes, na qual
os salários apresentaram média igual a 3,6 mil reais e
desvio-padrão igual a 0,5 mil reais. O pesquisador sabe
que, na sua população de gerentes, o tempo médio de
experiência no cargo é igual a 12 anos, enquanto que, na
sua amostra, o tempo médio de experiência no cargo
encontrado foi de 8 anos. Sabendo-se da forte relação
linear entre o salário e o tempo de experiência no cargo, o
pesquisador decidiu usar um estimador de regressão para
o salário médio. Para tanto, ajustou nos dados da amostra
um modelo de regressão linear do salário (Y, em mil reais)
em função do tempo de experiência no cargo (x, em anos),
obtendo a equação estimada

A estimativa de regressão para o salário médio é
Uma indústria mineradora produz minério de ferro e tem
um contrato com uma siderúrgica, especificando que o
teor médio de ferro nos lotes de minério entregue a ela
deve ser de, no mínimo, 60%. Caso contrário, os lotes são
devolvidos e a mineradora deve pagar uma multa. Para
certificar-se de que está enviando minério de ferro dentro
do que foi especificado no contrato, a mineradora toma
amostras de minério de cada lote a ser embarcado. Em
seguida, determina o teor médio de ferro do minério de
cada lote. A mineradora gostaria que a probabilidade de
concluir o lote a ser enviado cumprisse as especificações
estabelecidas pela siderúrgica quando, na verdade, não
as cumpre, seja, no máximo, 0,025. Considere as quatro
hipóteses a seguir:
Hipótese 1: o teor médio de minério de ferro do lote é
maior do que 60%.
Hipótese 2: o teor médio de minério de ferro do lote é
maior ou igual a 60%.
Hipótese 3: o teor médio de minério de ferro do lote é
menor do que 60%.
Hipótese 4: o teor médio de minério de ferro do lote é
menor ou igual a 60%.
Considerando as informações apresentadas, as hipóteses
nulas e a alternativa do teste a ser realizada antes do
embarque do lote são, respectivamente, as hipóteses
Para um conjunto de dados, utilizou-se um programa de
computador para calcular o valor das médias aritméticas
simples, harmônica e geométrica. No entanto, os valores
resultantes dos cálculos foram impressos sem qualquer
identificação sobre a qual medida-resumo eles se referiam.
Os valores impressos foram 2.63, 2.46 e 2.25. Conhecendo
as propriedades dessas medidas-resumo, é correto afirmar
que os valores da média aritmética simples, harmônica e
geométrica são, respectivamente,
O modelo de regressão logística é um caso particular de
um modelo linear generalizado em que o componente
aleatório tem distribuição Bernoulli e a função de ligação é
a logito. Diante do exposto, marque V para as afirmativas
verdadeiras e F para as falsas.
( ) Para uma variável explicativa numérica, o modelo
logístico tem uma forma linear para o logito da
probabilidade:

ou seja, π(x ) aumenta ou diminui como uma função
linear de x.
( ) A chance ou odds é a razão entre as probabilidades
de sucesso e fracasso e pode ser expressa como
e α(eβ)x. Quando a variável explicativa aumenta em uma unidade, a chance é aumentada multiplicativamente
por β.
( ) Para a avaliação do modelo de regressão com variáveis
explicativas numéricas pode-se utilizar a estatística X²
de Pearson ou a estatística G² do teste da razão de
verossimilhança dadas, respectivamente, por:

( ) Para a análise de resíduos de um modelo de regressão
logística com variáveis explicativas numéricas pode-se
utilizar o resíduo de Pearson ou o resíduo ajustado de
Pearson, dados, respectivamente, por:
imaegm
( ) O modelo de regressão logística multicategorizada é
uma generalização do modelo de regressão logística,
onde a variável resposta assume mais de duas categorias.
Quando as categorias são nominais, escolhe-se
uma como sendo a base para se construir as chances e
fazer as análises necessárias. No caso de categorias
ordinais, a ordenação pode ser incorporada ao modelo
na forma de probabilidades acumuladas, obtendo-se,
então, o modelo logito acumulativo.
A sequência está correta em
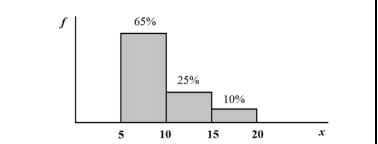
Com referência à figura acima, que mostra a distribuição da renda
mensal — x, em quantidades de salários mínimos (sm) — das
pessoas que residem em determinada região, julgue os itens
subsequentes.
O histograma da variável x apresenta as densidades de frequência em cada classe.
Pedro e João são os oficiais de justiça no plantão do fórum
de determinado município. Em uma diligência distribuída a Pedro,
X é a variável aleatória que representa o sucesso (X = 1) ou
fracasso (X = 0) no cumprimento desse mandado. Analogamente,
Y é a variável aleatória que representa o sucesso (Y = 1) ou
fracasso (Y = 0) de uma diligência do oficial João.
Com base nessa situação hipotética e considerando a soma
S = X + Y, e que P(X = 1) = P(Y = 1) = 0,6 e E(XY) = 0,5, julgue
os itens que se seguem, acerca das variáveis aleatórias X, Y e S.
A média da distribuição S é igual a 1,2.
As quantidades diárias de processos administrativos (N )
protocolados em certo órgão público seguem uma distribuição de
Poisson com média igual a 5. Cada processo protocolado é
encaminhado para a superintendência A ou para a B e, assim, a soma
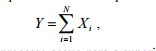
em que Xi = 1 se o processo segue para a superintendência A, e Xi = 0 se o processo segue para B, representa o total diário de
processos administrativos protocolados que se destinam para a
superintendência A.
Com base nessa situação, julgue os seguintes itens considerando
que X1, X2, ..., XN sejam variáveis aleatórias independentes, e que
P(X1 = 1) = P(X2 = 1) = ... = P(XN = 1) = 0,8.
A reta de regressão linear de Y em N = n é E(Y | N = n) = 0,8n.
Considerando a função de densidade conjunta na forma f(x, y) = c,
em que 0 < x < y < 1 e c > 0 é uma constante de normalização,
julgue os seguintes itens.
As variáveis aleatórias X e Y são independentes.

