A probabilidade de que um evento resulte em sucesso é p. Seja X a variável aleatória que representa o número de repetições independentes do evento até que ocorram dois sucessos. Sabendo-se que a probabilidade de X ser igual a 4 é igual à probabilidade de X ser igual a 5, a variância de X é igual a
Considere as seguintes afirmações:
I. A análise fatorial é, geralmente, aplicada sobre variáveis métricas, apesar de existirem métodos especiais para o emprego dessa técnica a variáveis dicotômicas.
II. Na análise discriminante, a variável dependente deve ser não métrica e as variáveis independentes devem indicar diferenças entre, pelo menos, dois grupos.
III. A análise de correspondência não é adequada para pesquisa aleatória e não é sensível a observações atípicas.
IV. Na análise de agrupamentos, as medidas de similaridade mais utilizadas são as correlacionais.
Está correto o que consta APENAS em

O valor da mediana de X adicionado ao valor da mediana de Y é igual a
Em uma pescaria, os pescadores Alberto, Bruno e Carlos
colocavam os peixes que pescavam em um mesmo recipiente. Ao
final da pescaria, o recipiente continha 16 piaus e 32 piaparas. Na
divisão dos peixes, cada um deles afirmou que teria pescado mais
peixes que os outros dois.
Julgue os itens a seguir, a respeito dessa situação.
Considere que a discussão tenha sido assistida por 9 amigos de Alberto; 8 amigos de Bruno; e 8 amigos de Carlos; dos quais 3 eram amigos apenas de Alberto; 1 era amigo apenas de Bruno; 2 eram amigos apenas de Carlos; 2 eram amigos apenas de Alberto e Carlos. Nessa situação, é correto afirmar que, entre os que assistiram à discussão, a quantidade de amigos de Bruno e Carlos era superior à quantidade de amigos de Alberto ou Bruno.
Os dados de uma pesquisa são agrupados em classes e apresentados no histograma a seguir. Sabe-se que as classes possuem a mesma amplitude e que o limite inferior da primeira classe e o limite superior da última classe valem, respectivamente, 10 e 90.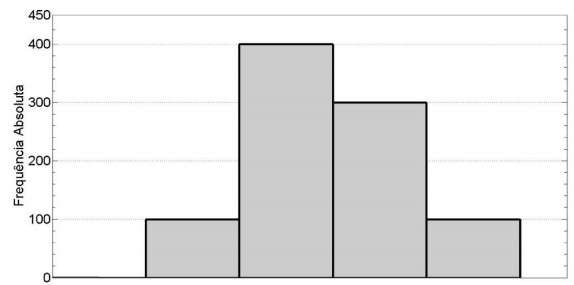
Utilizando o método da interpolação linear, o valor aproximado da mediana é
Um eletrodoméstico é vendido por R$ 1.200,00 (mil e duzentos reais) sem entrada e em 3 parcelas fixas de R$ 400,00. O mesmo eletrodoméstico pode ser vendido à vista por R$ 1.100,00 (mil e cem reais). Antônio comprou o eletrodoméstico à vista com dinheiro que retirou de uma aplicação com juros compostos à taxa de 2% ao mês. A economia de Antônio nessa compra em relação ao valor parcelado foi de aproximadamente
Uma pessoa faz uma aplicação de quatro meses a juros compostos (taxa de 2% ao mês) para quitar uma dívida de R$ 20.000,00 (vinte mil reais). O menor valor que deve ser investido para efetuar o pagamento da dívida é
Observe a amostra a seguir:
1,2 1,7 2,1 2,2 2,2 2,3 2,4 2,4 2,5 2,5 2,5 2,5 2,6 2,7 2,8
3,0 3,0 3,5 3,8 4,5 6,0 6,8 7,5 7,5 7,6 7,8 8,0 8,0 8,2 10,0
Supondo um eixo cartesiano horizontal usual, o Box-plot
correspondente a esses dados é melhor representado por:
Considere uma amostra aleatória X1, X2, X3, X4 de uma variável
aleatória populacional com média μ e os seguintes estimadores
de μ:
T1 = (X1 + X2 + X3 + X4)/4
T2 = (X1 + X2 + X3)/3
T3 = X1
Se EQM1, EQM2 e EQM3 são os erros quadráticos médios de
T1, T2 e T3 em relação a μ, respectivamente, então
Uma variável aleatória X tem função de densidade de probabilidade dada por f(x) = x–2, se x > 1, f(x) = 0, se x ≤ 1. A média de X é
Uma amostra X1 , X2 , ... X10 , de tamanho 10, de uma variável
populacional N(μx , σx2) será observada e uma amostra Y1 , Y2 , ... Y10 , de tamanho 10, de uma variável populacional N(μY, σy2), independente da amostra X, será também observada.
O problema é testar H0: σx2 ≤ σy2 contra H1: σx2 > σy2.
Para tal, será usada a estatística de teste a seguir
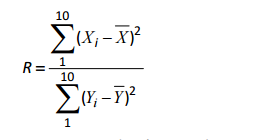
e um critério de decisão que rejeita a hipótese nula se R > k.
Ao nível de significância de 5%, k é igual a
Avalie se as distribuições de probabilidade a seguir pertencem
à família exponencial.
I. Gaussiana inversa parâmetros μ e σ2.
II. Poisson parâmetro λ.
III. Uniforme no intervalo [0, θ].
Assinale
Em relação à amostragem estratificada, assinale a afirmativa incorreta.
Num concurso público composto por 3 fases o critério de aprovação de um candidato depende da média e do desvio padrão. A média e o desvio padrão de um candidato que na 1a fase obteve 72 pontos, na 2a fase obteve 68 pontos e na 3a fase obteve 73 pontos são, respectivamente:
A distribuição de frequência, conforme tabela abaixo, representa os valores de imposto pagos pelos funcionários de
uma empresa, em certo mês.
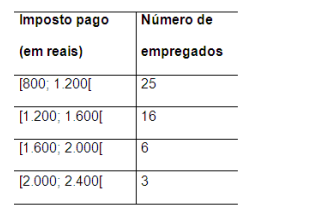
O valor médio do imposto pago pelos funcionários, nesse mês, foi de:

