Com base em distribuições contínuas, julgue os itens subsequentes.
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
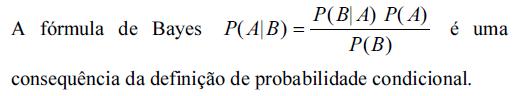
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
Considerem os eventos A = trabalhador recebe mais que um salário mínimo e B = o trabalhador é do sexo feminino. Nesse contexto, se a probabilidade de, em uma população, uma pessoa escolhida ao acaso ser um homem que recebe até um salário mínimo é 1/3, então a probabilidade de uma pessoa selecionada ao acaso ser do sexo feminino ou receber mais que um salário mínimo é superior a 1/2.
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral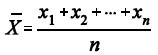 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
A razão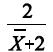 
é um estimador do parâmetro p obtido utilizando-se o método dos momentos.
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral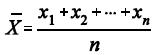 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
A média amostral é um estimador não tendencioso para a média populacional de empregados não registrados por microempresas.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
Estima-se que variância da distribuição Y, utilizando-se o método da máxima verossimilhança, seja igual a 0,7.
Considerando que as propriedades da estatística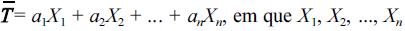 
representa uma
amostra aleatória simples de tamanho n, retirada de uma população
X com média µ, e que a1, a2, ..., an, são constantes positivas tais que
a1+a2+an= 1, julgue os itens que se seguem.
Se a1 < a2 < ... < an, então a estatística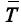 
será um estimador tendencioso da média populacional &nicro;.
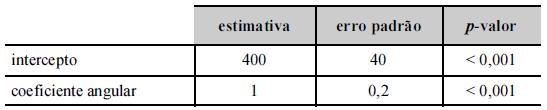
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
Com 95% de confiança, a estimativa intervalar para o coeficiente angular é, aproximadamente, igual a 1,0 ± 0,2.
Um modelo de regressão linear múltipla, que foi ajustado em uma perícia judicial, possui 11 variáveis explicativas. O tamanho da amostra nessa modelagem foi igual a 101. A soma de quadrados total foi igual a 15.000 e a soma de quadrados residual foi igual a 5.000. Com base nessas informações, julgue os próximos itens.
O coeficiente de determinação R2 do modelo de regressão linear múltipla é superior a 70%.
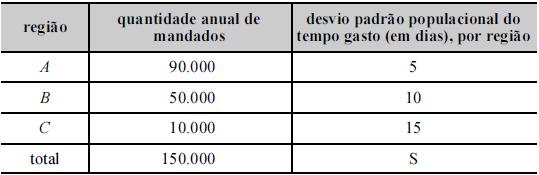
Um levantamento estatístico por amostragem probabilística
foi realizado para se estimar o tempo médio, em dias, gasto por
oficiais de justiça no cumprimento de mandados judiciais. Nesse
levantamento, os mandados foram divididos de acordo com a
localização geográfica do intimado. A tabela acima mostra a
quantidade anual de mandados para cada região, os valores dos
desvios padrão da variável de interesse por região e S, que
representa o desvio padrão populacional do tempo gasto.
Considerando que o total de mandados judiciais utilizados no
levantamento tenha sido igual a 400, julgue os itens de
O desvio padrão populacional S é igual a 10 dias.
Durante um período de 50 dias, observou-se a quantidade de determinada ocorrência por dia em uma indústria. O número de dias (fi) em que aconteceram i ocorrências (0 ≤ i ≤ 4) pode ser encontrado com a utilização da fórmula fi = -i2 + 6i + 4. Obtendo os respectivos valores da média aritmética (Me), da mediana (Md) e da moda (Mo), da quantidade de ocorrências por dia, então é correto afirmar que
Em 100 experiências realizadas ao acaso, independentemente, para apurar o valor de uma constante física, obteve-se uma média de 3,7 para esta constante. Admite-se que a distribuição da população dos resultados é normalmente distribuída, de tamanho infinito, com média µ e com uma variância populacional igual a 0,16. Considere na curva normal padrão (Z) as probabilidades P(Z > 1,64) = 0,05 e P(Z > 1,96) = 0,025. Com base na amostra inicial de 100 experiências, obtém-se que o intervalo de confiança ao nível de 95% para µ é
O número de automóveis alugados por uma locadora de veículos, que não funciona nem sábado nem domingo, durante os dias de uma determinada semana, está indicado pela tabela abaixo. Deseja-se testar a hipótese se o número de automóveis alugados não depende do dia da semana, com a utilização do teste de qui-quadrado e adotando, como frequência esperada por dia, a média diária realizada na semana.
Verificou-se que o qui-quadrado observado (Q) apresentou um valor inferior ao valor do qui-quadrado tabelado para o nível de significância de 5% com o respectivo número dos graus de liberdade. É correto afirmar, então, que ao nível de significância de 5%, a conclusão do teste é que o número de automóveis alugados
Considerando a equação da reta obtida pelo método dos mínimos quadrados, a previsão do primeiro ano em que a venda irá superar R$ 60.000,00 será em
