Sobre o modelo de fatores ortoganais, é correto afirmar que
Sobre planos de amostragem (PA) para controle estatístico de qualidade é correto afirmar que em PA
Para uma população de 10 indivíduos é retirada uma amostra de 3 indivíduos, sem reposição. Assim, o número de amostras possíveis é
Os produtos da empresa Puzo apresentam distribuição normal com peso médio de 30 kg e desvio-padrão de 6 kg. Para testar a qualidade do seu produto, a empresa tomou uma amostra de 49 produtos, obtendo uma média amostral de 32 kg. A estatística de teste Z utilizada no teste de hipóteses de qualidade é
Seja V o vetor [-8, 10]. O módulo de V é
A média harmônica dos 4 primeiros números primos maiores que 3, com aproximação de duas casas decimais, é
O valor absoluto da diferença entre a média geométrica e a média aritmética de X = {2, 2, 2, 2, 4, 16, 128, 128} é
A equipe de pesquisa de um laboratório farmacêutico está desenvolvendo um medicamento analgésico que promete aliviar a dor de cabeça em um tempo médio menor do que o tempo gasto pelo medicamento padrão, que é de 15 minutos, em média. Para liberar o novo medicamento com essa promessa, é necessário executar um experimento e analisar os dados coletados. Depois de planejar e executar o experimento com a nova droga, coletar os dados e processá-los, o teste estatístico apropriado, que adotou uma hipótese alternativa unilateral, resultou em um valor-p (ou probabilidade de significância) igual a 0,028. Na definição das hipóteses do teste, levou-se em conta que o erro de liberar o medicamento com uma falsa promessa de redução no tempo de alívio da dor de cabeça é mais grave do que deixar de liberar um novo medicamento que funcione em um tempo menor. Denotando por µ o tempo médio, em minutos, para o alívio da dor de cabeça do novo medicamento, considere que
I. as hipóteses nula e alternativa do teste estatístico são, respectivamente, (µ ≥ 15) e (µ < 15).
II. adotando-se um nível de significância de 0,05, há evidências estatísticas suficientes contra a hipótese nula do teste.
III. se a hipótese alternativa do teste fosse bilateral, o valor- p seria igual a 0,014.
Assinale
Para duas variáveis x e y, são dados: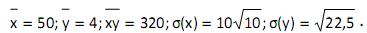 
O coeficiente de correlação entre as variáveis é
Na análise de regressão múltipla foram encontrados:
soma dos quadrados da regressão: 40.000.
soma dos quadrados dos erros: 10.000.
Assim, o coeficiente de determinação múltipla (R2 ) dessa regressão é
Com relação a estatística, julgue os itens seguintes.
Considere que a covariância e a correlação linear entre as variáveis X e Y sejam, respectivamente, iguais a 5 e 0,8. Suponha também que a variância de X seja igual a quatro vezes a variância de Y. Nesse caso, é correto afirmar que a variância de X é igual a 2.
O tempo total de montagem de uma peça mecânica tem distribuição normal e é dado pela soma dos tempos das 3 etapas necessárias para a sua conclusão. Sejam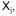 
, i = 1, 2, 3, as variáveis aleatórias que representam os tempos de montagem das etapas 1, 2 e 3, respectivamente. Sabe-se que essas variáveis são independentes e que têm distribuição normal com parâmetros dados na tabela abaixo: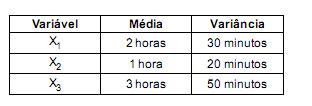 
A probabilidade de a peça levar entre 374 e 384 minutos para ser montada é igual a
Seja X uma variável aleatória contínua com função densidade de probabilidade dada por: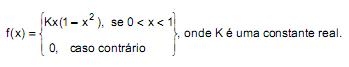 
Sendo Mo(X) = moda da variável X e a = [Mo(X)] 2, então P(X < a) é igual a
Considere
I. O coeficiente de variação de uma variável aleatória X que tem distribuição qui-quadrado com n graus de liberdade é igual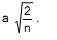 
II. Se X e Y são variáveis aleatórias independentes, X sendo normal padrão e Y tendo distribuição qui-quadrado com n graus de liberdade, então a variável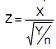
tem distribuição t de Student com (n - 1) graus de liberdade.
III Se X tem distribuição gama com parâmetros a e ß, então a média de X é igual a aß.
IV. Se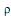 
é o coeficiente de correlação linear de Pearson entre as variáveis aleatórias X e Y e se Z = aX e W = bY, onde a < 0 e b > 0 (a e b são constantes), então o coeficiente de correlação linear de Pearson entre as variáveis aleatórias Z e W é ab
.
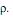Está correto o que se afirma em
De 30 caminhões de entrega de encomendas de uma grande loja de departamentos, 6 emitem excesso de poluentes. Selecionam-se aleatoriamente e sem reposição uma amostra de n caminhões para a inspeção de poluentes. Seja X a variável aleatória que representa o número de caminhões com excesso de poluentes na amostra. Sabendo-se que a média de X é 2,4, o valor de n é
