Para testar H0: μ ≤μ0 versus H1: μ > μ0, em que μ é a média
populacional de uma variável N(μ, σ2), uma amostra aleatória de
tamanho 16 será obtida.
O teste t-Student usual rejeitará H0 ao nível de significância de
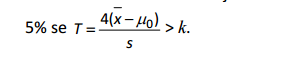
O valor de k é igual a
Uma reta de regressão linear simples foi ajustada por mínimos
quadrados e os resíduos ei = yi -y^i e foram computados:
0,1 0,5 1,2 0,4 0,8 1,0 1,0 0,6
Supondo que os resíduos são normalmente distribuídos com
média 0 e variância σ2, a estimativa de σ2 é igual a
INSTRUÇÃO – As questões 38 e 39 devem ser respondidas com base no caso YGOR
LTDA, descrito abaixo.
A empresa YGOR LTDA pretende analisar os índices de adimplência de seus clientes
que compram a prazo. A tabela abaixo apresenta uma amostra de 40 clientes da
empresa, com seus índices de adimplência para cinco períodos (A, B, C, D e E) e a soma
dos cinco períodos.
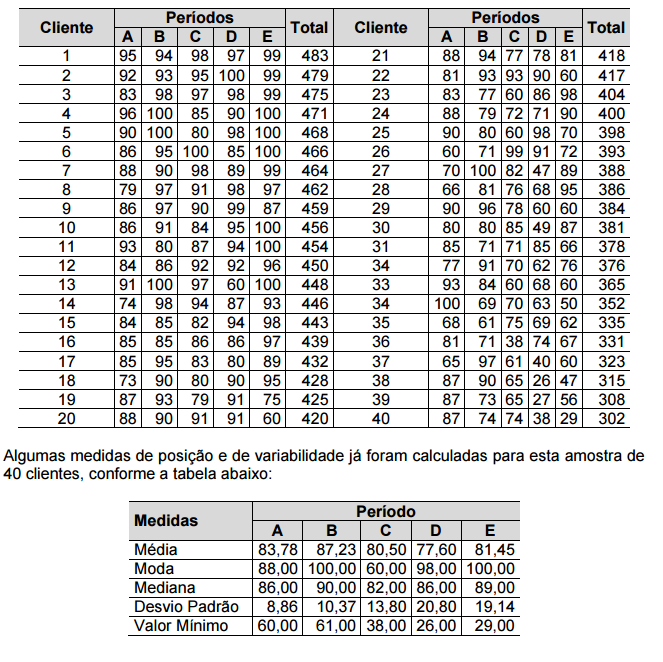
Considerando-se os 10 primeiros clientes, apenas para o período A, os valores para as medidas
de posição e de variabilidade mencionadas no caso YGOR podem ser diferentes.
Sobre medidas de posição e de variabilidade para toda a amostra e apenas para os 10 primeiros
clientes, no período A, é CORRETO afirmar que
Observe atentamente os dados apresentados na tabela a seguir.
Assumindo a variável X como independente, o coe?ciente angular da reta de mínimos quadrados ajustada a esses dados vale:
Atenção: Para resolver as questões de números 21 e 22 considere a tabela abaixo, referente à distribuição de frequências relativas
dos salários dos 400 empregados de uma empresa no mês de agosto de 2013, sabendo-se que (m + n) = 10%.

O valor da média aritmética dos salários dos empregados foi obtido considerando-se que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio deste intervalo. O número de empregados correspondente ao intervalo de classe a que pertence o valor da média aritmética é igual a
Seja Xi um elemento de uma população de tamanho 20, com 1 = i = 20. Sabe-se que

O coeficiente de variação desta população apresenta um valor c, tal que
Considere que E = (m-1)X - mY + 2Z corresponde a uma classe de estimadores não viesados da média µ de uma população normalmente distribuída com variância σ2 ≠ 0. (X, Y, Z) é uma amostra aleatória, com reposição, desta população com m sendo um parâmetro real. O estimador mais eficiente desta classe apresenta uma variância igual a
Uma amostra aleatória de 361 empregados foi extraída, sem reposição, de uma empresa com 1090 empregados, apurando-se um intervalo de confiança ao nível de (1-α) para a média da população dos salários da empresa, em R$, igual a [4.956,80 ; 5.043,20]. Considere que a distribuição desta população é normal com um desvio padrão populacional igual a R$ 627,00 e que na curva normal padrão (Z) a probabilidade P(-m ≤ Z ≤ m) = (1-α), com m > 0. Com base no intervalo encontrado pela amostra, tem-se que m é igual a
Em 3 empresas (X, Y e Z) foram escolhidos por sorteio, em cada uma, 12 operários para realização de um treinamento. Após o treinamento, foi realizado um teste, independentemente, com todos estes 36 operários e deseja-se saber, ao nível de significância de 5%, se as médias das respectivas notas dos grupos formados por cada empresa são iguais. Pelo quadro de análise de variância, verificou-se que a soma de quadrados referente à fonte de variação entre grupos representou 47,2% da fonte de variação total. O valor da estatística F (F calculado) utilizado para comparar com o F tabelado (distribuição F de Snedecor), com o objetivo de verificação da igualdade das médias, é
Sejam f (k) e g (k) as funções de autocorrelação e autocorrelação parcial de um processo de médias móveis de ordem 1, MA (1), com parâmetro de médias móveis igual a 0,5. Nessas condições, é correto afirmar que
U ma empresa produz componentes de dois tipos: A e B. Sejam as variáveis aleatórias:
X = tempo de vida do componente A, em horas e Y = tempo de vida do componente B, em horas. De um lote de 120 componentes do tipo A e 80 componentes do tipo B, retira-se ao acaso um componente. Sabendo-se que X tem distribuição exponencial com média de 1.000 horas e que Y tem distribuição exponencial com média de 700 horas, a probabilidade do componente selecionado ter duração inferior a 1.400 horas é

A função de distribuição acumulada da variável aleatória X, no intervalo [0, 1], é dada por:
F(x) = 3x2 - 2x3.
Se Mo é a moda da variável X, então P (0,2 ≤ X ≤ Mo) é igual a
A seguinte figura ilustra o diagrama de dispersão das grandezas X e Y: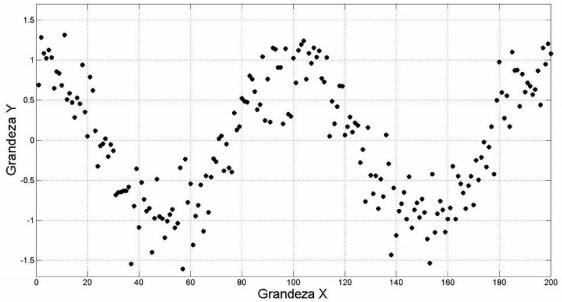
Qual método de regressão deve ser utilizado para as Grandezas X e Y?
Zt e Wt são séries temporais modeladas por processos autorregressivos de primeira ordem AR(1), cujos coeficientes de regressão ou parâmetros dos processos AR(1) valem, respectivamente, 0,99 e 0,01, e variâncias dos ruídos brancos iguais a 1. As seguintes figuras ilustram realizações típicas das séries Zt e Wt, não necessariamente nessa ordem.
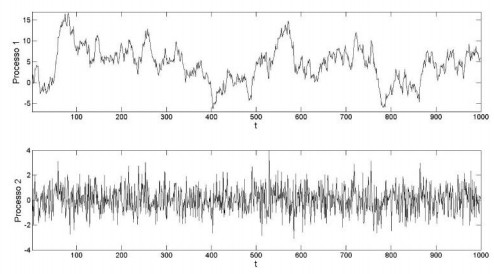
O processo que representa a realização de Zt e o valor de ρ = E [ZZt ZZt-1], em que E[ ] denota o operador valor esperado, são



