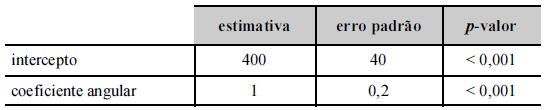
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
Em relação ao teste de hipóteses H0: α= 0 versus H1 : α ≠ 0, em que α representa o intercepto, a hipótese nula deve ser rejeitada caso se adote o nível de significância de 1%.
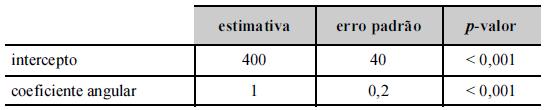
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
Os resultados apresentados na tabela sugerem um bom ajuste, já que as estimativas dos coeficientes foram todas significativas com p-valores inferiores a 0,1%.
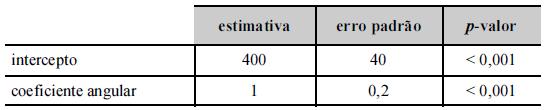
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
Caso se faça um ajustamento utilizando-se o método da máxima verossimilhança, a estimativa do coeficiente angular sofrerá alteração e a do intercepto permanecerá a mesma.
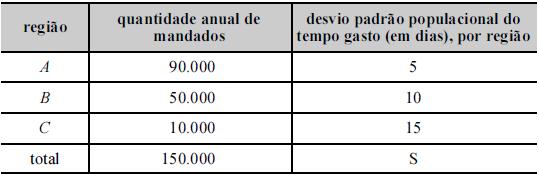
Um levantamento estatístico por amostragem probabilística
foi realizado para se estimar o tempo médio, em dias, gasto por
oficiais de justiça no cumprimento de mandados judiciais. Nesse
levantamento, os mandados foram divididos de acordo com a
localização geográfica do intimado. A tabela acima mostra a
quantidade anual de mandados para cada região, os valores dos
desvios padrão da variável de interesse por região e S, que
representa o desvio padrão populacional do tempo gasto.
Considerando que o total de mandados judiciais utilizados no
levantamento tenha sido igual a 400, julgue os itens de
Na amostragem aleatória estratificada com alocação uniforme, o total de observações na região C foi igual ou superior a 160.
Dois alunos obtiveram escores reduzidos (graus expressos em unidades de desvio padrão) iguais a 0,6 e -1,0 em uma prova de matemática.Sabendo-se que seus graus foram 74 e 42, um terceiro aluno com grau 62 tem grau reduzido igual a:
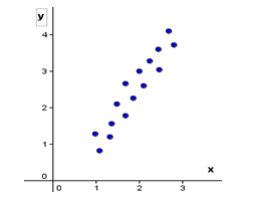
Considerando os dados descritos na "nuvem de pontos" do gráfico abaixo, o valor que mais se aproxima do
coeficiente de correlação de Pearson é:
A durabilidade, em centenas de horas, de máquinas sem necessidade de manutenção é dada pela seguinte tabela.

De acordo com a tabela o ponto médio da classe mediana , em horas, é igual a:
Considerando os dados da tabela, pretende–se retirar uma amostra proporcional estratificada de 40% da população.

Nessas condições deve–se considerar uma amostra de:
As frequências absolutas das estaturas de todos os funcionários de uma empresa estão distribuídas de acordo com
a tabela abaixo:
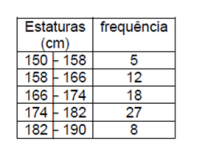
De acordo com a distribuição acima, a alternativa que apresenta respectivamente a frequência relativa acumulada da
classe modal é, aproximadamente:
O quadro indica os salários dos funcionários de certa empresa:
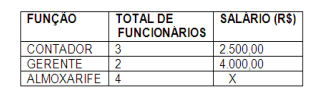
Se a média de salário desses funcionários é de R$ 2.700,00 então o salário X de cada almoxarife dessa empresa é,
em reais, de:
A tabela a seguir apresenta algumas estatísticas descritivas
do “peso" e do “comprimento" de 20 sapos.

É correto afirmar que os sapos têm
Uma cidade tem 12.000 domicílios divididos em três bairros (denotados por B1, B2 e B3), que pagam IPTU em três faixas
de valores (denotadas por I1, I2 e I3). Sabe-se que um pesquisador deseja estimar a média da renda mensal destes
domicílios via Amostragem Estraficada ou Amostragem por Conglomerados de 1.200 domicílios. O quadro a seguir
mostra o número de domicílios e a variância da renda mensal em cada faixa de IPTU e em cada bairro. A variância da
renda mensal entre todos os domicílios da região é igual a 3.400 (variância global).

Com o objetivo de aumentar a precisão do estimador da média da renda mensal, é correto afirmar que
indústria de confecções suspeita que as peças de tecido recebidas de uma fábrica, ao longo dos cinco dias da semana,
não são homogêneas quanto à resistência das fibras à tensão depois da tintura. Para verificar essa suspeita, uma amostra
de 9 peças de tecido de cada um dos cinco dias da semana foi avaliada quanto à resistência das fibras à tensão depois da
tintura. Os resultados da análise apropriada e aplicada a esses dados estão resumidos na tabela a seguir.

Considerando que μi
é a média da resistência à tensão do lote do dia i, i = 1, 2, 3, 4, 5, analise.
I.A hipótese nula do teste envolvido na análise desses dados é a de que μ1 = μ2 = μ3 = μ4 = μ5.
II.A hipótese alternativa do teste envolvido na análise desses dados é a de que μ1 ≠ μ2 ≠ μ3 ≠ μ4 ≠ μ5.
III.A hipótese alternativa do teste envolvido na análise desses dados é a de que pelo menos um dia da semana tem lote
com resistência média diferente da resistência média dos lotes dos demais dias da semana.
IV.A probabilidade de concluir erroneamente pela existência de diferença na resistência média à tensão dos lotes em ao
menos um dos dias da semana é de 0,058.
Está( ão) correta( s) apenas a( s) afirmativa( s)
O efeito de uma campanha publicitária para promoção
do voluntariado nas eleições será avaliado por meio do
seguinte experimento: antes do início da campanha, um
grupo de 200 eleitores responderá à seguinte questão:
“você gostaria de ser voluntário nas próximas eleições?
(sim ou não)". A campanha será lançada e, após três meses
de veiculação em rádio e TV, o mesmo grupo de eleitores
responderá à mesma questão. A campanha será reforçada
com publicidade em outdoors nos próximos três meses e,
após esse período, o mesmo grupo de eleitores responderá
novamente à mesma questão. A equipe responsável
pelo estudo deseja comparar o percentual de eleitores que
desejam ser voluntários nas próximas eleições em cada
etapa. Considerando o planejamento do experimento e o
tipo de variável a ser observada, o teste estatístico mais
adequado para avaliar a hipótese de estudo é o
“A análise de resíduos de um modelo de regressão linear
múltipla pode ser utilizada para verificar se o modelo se
adequa aos dados. Nesse sentido, gráficos e testes ajudam
a identificar discrepâncias entre os valores observados da
variável resposta e os valores preditos pelo modelo." De
acordo com o trecho anterior, marque V para as afirmativas
verdadeiras e F para as falsas.
( ) Quando os pontos do diagrama de dispersão do resí-
duo padronizado versus variável explicativa apresentar
uma tendência, a inclusão do logaritmo da variável
explicativa pode melhorar o modelo.
( ) Quando os pontos do diagrama de dispersão do resí-
duo versus variável omitida no modelo apresentar
uma tendência linear, a inclusão da variável omitida
pode melhorar o modelo.
( ) Quando o desenho esquemático (boxplot) dos resí-
duos padronizados apresentar observações além dos
limites superior ou inferior, existe uma forte indicação
da presença de outliers que devem ser investigados.
( ) Quando o desenho esquemático dos resíduos tem a
distância entre a mediana e o primeiro quartil e a
distância entre a mediana e o terceiro quartil bem distintas,
existe uma forte indicação de que a distribuição
das observações são assimétricas e o componente
aleatório do modelo pode não ter distribuição normal.
( ) A suposição de homocedasticidade dos resíduos pode
ser avaliada através de: teste de Levéne; teste de
Brown & Forsythe; gráfico de resíduos versus valores
preditos pelo modelo; gráfico do resíduo versus cada
uma das variáveis incluídas no modelo.
A sequência está correta em

