Os resultados de uma pesquisa são apresentados parcialmente na seguinte tabela:
Sabe-se que a média é a mediana valem, respectivamente, 1,2 e 2. Os valores de X e Y que atendem a tais condições são
Os modelos lineares generalizados vêm se tornando fundamentais na área de análise estatística por unificarem vários procedimentos estatísticos e por apresentarem excepcionais características de desempenho em várias aplicações. Tais modelos pressupõem que a variável de resposta possui uma distribuição pertencente à família exponencial, definida pela seguinte expressão:
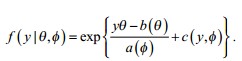
Nessa expressão θ e ø são escalares e a (ø), b (θ) e c(y,ø) são funções reais. Várias distribuições conhecidas podem ser expressas da forma da equação acima, como, por exemplo, a gaussiana. Para uma gaussiana de média 1 e variância 0,1, o valor de a(ø)+2xb+c(y,ø)é
Em uma pescaria, os pescadores Alberto, Bruno e Carlos colocavam os peixes que pescavam em um mesmo recipiente. Ao final da pescaria, o recipiente continha 16 piaus e 32 piaparas. Na divisão dos peixes, cada um deles afirmou que teria pescado mais peixes que os outros dois.
Julgue o item a seguir, a respeito dessa situação.
Na situação dada, se 2 peixes fossem retirados do recipiente, aleatoriamente, a probabilidade de que pelo menos um fosse um piau seria maior que 1⁄2.
Com base nos conceitos de probabilidade, julgue os itens seguintes.
Considere três eventos (A, B e C), de modo que A depende de B, mas não de C, e B depende de C. Nessa situação, se P(A ∩ B ∩ C) = sub, sup { font-size: 0.6em;} 1⁄4, P(B) = sub, sup { font-size: 0.6em;} 3⁄5 e P(C) = sub, sup { font-size: 0.6em;} 5⁄8 então P(A | B) = sub, sup { font-size: 0.6em;} 2⁄3.
Julgue o item abaixo, a respeito de técnicas de amostragem.
Em uma amostragem sistemática cuja fração de seleção seja igual a 3 e o tamanho resultante da amostra seja igual a 125.000 observações, o tamanho da população será superior a 300.000 elementos.
Com relação à teoria de probabilidades, julgue os próximos itens.
Caso os eventos A e B sejam tais que P(A) > P(B) e P(B*A) = 1/3, então P(AB) > 0,30.
No que se refere a distribuições discretas, julgue os seguintes itens.
Para a distribuição de probabilidades P(X = k) = 2-k, em que k = 1, 2, ..., a média e a variância são iguais a 2.
Com base em distribuições contínuas, julgue os itens subsequentes.
Se P for uma variável aleatória beta com parâmetros (a, b) e se X for uma binomial com parâmetros N e P, então o produto de (P) × P(X), em que f(P) é a função densidade de probabilidade de P e P(X) é a probabilidade de X, será proporcional à densidade de uma beta com parâmetros (a + X, b + N X).
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
Considere que, em um tribunal, os processos sejam classificados como urgentes (T1) e não urgentes (T2) e que os não urgentes sejam reclassificados como importantes (T2.1) ou não importantes (T2.2). Considere-se, ainda, que a proporção de processos do tipo T1 seja 0,5 e que, entre os processos do tipo T2, 0,2 sejam do tipo T2.1 e 0,8 do tipo T2.2. Se X, Y e Z forem, respectivamente, as contagens de processos de tipos T1, T2.1 e T2.2 em determinado momento, então a distribuição conjunta de (X, Y, Z) é uma multinomial com parâmetros 0,5, 0,1 e 0,4.
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
Todos os eventos independentes são disjuntos.
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral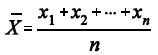 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
De acordo com o método de mínimos quadrados ordinários, a média amostral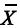 
é o estimador do parâmetro p.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
Considerando-se o estimador não viciado uniformemente de mínima variância (uniformly minimum-variance unbiased estimator), infere-se que P(Y = 0) é igual a 0,9970.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
As frequências relativas 0,5; 0,35; 0,10 e 0,05 são estimativas não viciadas das probabilidades P(Y = 0), P(Y = 1), P(Y = 2) e P(Y = 3), respectivamente.
Considerando que as propriedades da estatística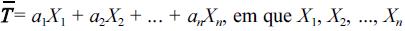 
representa uma
amostra aleatória simples de tamanho n, retirada de uma população
X com média µ, e que a1, a2, ..., an, são constantes positivas tais que
a1+a2+an= 1, julgue os itens que se seguem.
Se X seguir uma distribuição exponencial, então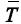 
será o
estimador não viciado uniformemente de mínima variância
(uniformly minimum-variance unbiased estimator) para
qualquer coleção de constantes positivas a1, a2, ..., an, tais que
a1 + a2+ ... + an = 1.
