Uma variável aleatória Gama é definida para valores reais
e positivos e sua função densidade é dada por
Diante do exposto, analise as afirmativas.
Estão corretas apenas as afirmativas
Em um departamento de uma empresa, o gerente decide dar um aumento a todos os empregados, dobrando o salário de todos eles.
Em relação às estatísticas dos novos salários, considere as afirmativas abaixo.
I - A média dobra.
II - A variância dobra.
III - A moda dobra.
É correto o que se afirma em
Um fabricante de peças automotivas sabe que a probabilidade de ocorrência de defeito de fabricação em uma peça corresponde a 5%. Assim, em um lote de 7.600 peças fabricadas, a média e o desvio padrão da distribuição de peças defeituosas serão, respectivamente, iguais a:
Com relação à teoria de probabilidades, julgue os próximos itens.
Se X1, X2, ..., Xn for uma amostra aleatória simples suficientemente grande e se Tn(X) for uma estatística qualquer, então a distribuição da amostra da estatística será normal.
No que se refere a distribuições discretas, julgue os seguintes itens.
Para distribuição conjunta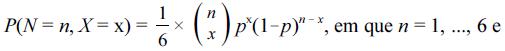 
.
Com base em distribuições contínuas, julgue os itens subsequentes.
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
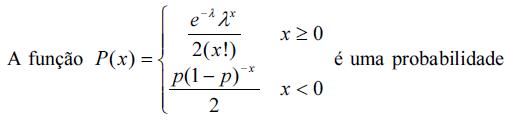
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
Os axiomas de Kolmogorov afirmam que a probabilidade da união de eventos é igual à soma das respectivas probabilidades.
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
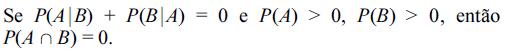
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral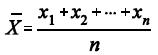 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
À medida que o tamanho da amostra aumenta, a média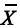 
converge quase certamente para uma distribuição normal padrão.
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral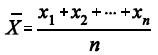 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
O erro padrão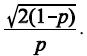 
.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
O erro padrão do estimador de máxima verossimilhança da probabilidade P(Y = 1) é igual a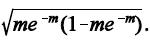 
Considerando que as propriedades da estatística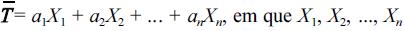 
representa uma
amostra aleatória simples de tamanho n, retirada de uma população
X com média µ, e que a1, a2, ..., an, são constantes positivas tais que
a1+a2+an= 1, julgue os itens que se seguem.
Na situação em que X seja a distribuição de Bernoulli e as constantes, tais que a1 = a2 = ... = an, a estatística n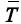
possuirá uma propriedade que se denomina suficiência.
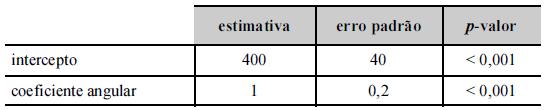
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
A correlação entre o valor do imóvel e a área construída do imóvel é igual a 1.
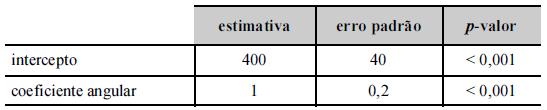
Um modelo de regressão linear simples foi ajustado pelo
método de mínimos quadrados ordinários como parte de um laudo
de avaliação imobiliária. Nesse modelo, cujos resultados se
encontram na tabela acima, a variável resposta y representa
o valor do imóvel, em R$ mil, e a variável regressora x é a
área construída do imóvel (em m2+a).
Considerando que o tamanho da amostra para essa modelagem
tenha sido superior a 500 e que os erros aleatórios pertinentes sejam
normais, julgue os itens a seguir.
O modelo ajustado foi y = x + 400, o que sugere que cada metro quadrado eleva, em média, R$ 1 mil no valor do imóvel.
