O modelo de componentes principais é utilizado para
representar a estrutura de variância-covariância em função
de um número reduzido de combinações lineares das
variáveis originais, com o objetivo de se ter uma redução
de dados e uma melhor interpretação destes. Para o vetor
aleatório X´ = [X1, X2, ∙∙∙, Xp] com matriz de covariância Σ e
autovalores iguais a λ1 ≥ λ1 ≥ ∙∙∙ ≥ λp ≥ 0, e as combinações
lineares:
Estão corretas apenas as afirmativas
Uma determinada indústria produz três produtos. A produção total é 1.000 unidades por mês.
O controle de qualidade da indústria registrou os seguintes números de peças defeituosas na produção:
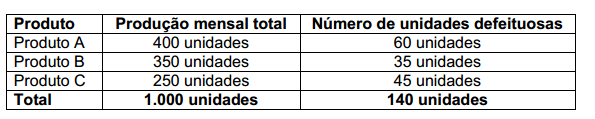
A probabilidade de encontrar uma peça defeituosa do produto B é de:
Uma sociedade empresária apresentou as seguintes estimativas de vendas de computadores:
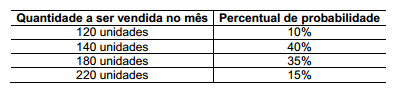
A quantidade esperada de unidades a serem vendidas no mês é de:
Um dos objetivos da estatística é sintetizar valores que uma ou mais variáveis podem assumir, para que tenhamos uma visão global da variação dessa ou dessas variáveis. Tabela é um quadro que resume um conjunto de observações que se compõe de: corpo, cabeçalho, colunas, linhas, casa ou célula e título. O (a )____________ posiciona-se na parte superior da tabela que especifica 0 conteúdo das colunas. Assinale a alternativa que preenche a lacuna corretamente.
É correto afirmar que se considera uma distribuição simétrica aquela que possui os mesmos valores para
Uma medida estatística comumente usada para a estimativa
de risco associado a aplicações em bolsas de valores,
ou fundos de ações é
O método de construção de testes de hipóteses é conhecido como procedimento clássico de teste de hipóteses
quando é fixada a probabilidade do erro do tipo I. Outro procedimento que pode ser adotado é aquele que consiste em
apresentar o nível descritivo ou valor-p, denominado de probabilidade de significância. Os passos são análogos ao
procedimento clássico – a principal diferença reside em não se construir a região crítica. Ao invés, indica-se qual a
probabilidade de ocorrerem valores da estatística mais extremos do que o observado, sob a hipótese de H0 ser
verdadeira. Suponha que uma estação de televisão afirma que 60% dos televisores estavam ligados no seu programa
especial em um dado dia da semana. Uma rede competidora deseja contestar essa afirmação e decide, para isso, usar
uma amostra de 200 famílias e conduzir o teste H0: π = 0,60 X H1: π < 0,60 . Selecionada a amostra, foram obtidos os
seguintes resultados: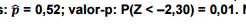 
Nesse contexto, assinale a alternativa correta.
Com relação à teoria geral da estimação de parâmetros, assinale a alternativa que corresponde a uma das propriedades desejáveis para um estimador.
Considere duas variáveis aleatórias, X1 e X2, independentes, e ambas normalmente distribuídas com média 2,00 e variância 8,00. Seja Y = X1X2. Assinale a alternativa correta que apresenta o valor do coeficiente de correlação entre X1 e Y.
Uma fábrica de pneus desconfiou que uma de suas máquinas estivesse com problema, pois a possibilidade de produzir um pneu defeituoso havia subido para 20%. A fim de inspecionar a linha de produção ao longo de um dia, a empresa contratou um consultor, que escolheu, ao acaso, 5 pneus para vistoriar. Assinale a alternativa que apresenta a probabilidade de o consultor ter escolhido um pneu sem defeito.
Considerando uma série temporal, é correto afirmar que
As idades de um grupo de indivíduos estão dadas a seguir:
20, 24, 32, 17, 45, 28, 31, 36, 40.
A mediana dessas idades é
Duas moedas honestas são lançadas. A probabilidade condicional de se obter duas “caras” sabendo que ao menos uma “cara” foi obtida é igual a
Se, para os dados da questão anterior, quisermos testar H0: p ≤ 0,6 versus H1: p > 0,6, ao nível de significância de 5%, a região crítica aproximada e a correspondente decisão serão: Use: √0,24 = 0,5
Sabe-se que um desvio padrão populacional é ≤ 10. O tamanho da amostra aleatória necessário para se possa garantir que P[ X - μ |< 0,4] = 0,95 é
