Binomial, Geométrica, Poisson, Exponencial e Gaussiana são algumas variáveis aleatórias muito empregadas na área de estatística. Com relação a essas variáveis são apresentadas as seguintes afirmativas:
I Diminuindo-se a média de uma variável aleatória Geométrica, diminui-se também a sua variância. Em particular, para uma média igual a 2, a variância dessa variável aleatória vale 2.
II Exponencial e Gaussiana possuem funções densidades de probabilidades completamente especificadas pela média.
III A variável aleatória Binomial pode ter média nula.
IV A variável aleatória Poisson pode ser empregada para aproximar uma variável aleatória Binomial, e essa aproximação tende a melhorar quando o número de realizações da variável aleatória aumenta.
É correto apenas o que se afirma em
Com relação aos modelos de processos utilizados na modelagem Box e Jenkins são apresentadas as seguintes afirmativas:
I Os processos AR podem ser representados por processos MA com ordem infinita.
II - Os processos AR, ARMA e MA são utilizados para modelar séries temporais não estacionárias.
III - A classe de modelos ARIMA pode descrever séries estacionarias e não estacionárias.
É correto apenas o que se afirma em
Dada a amostra: 2,0; 3,0; 1,0; 2,0; 2,0, o valor observado da variância amostral que é um estimador não tendencioso da variância populacional é igual a
Numa certa população, 505 das pessoas são do sexo feminino. Três pessoas dessa população serão aleatoriamente escolhidas, com reposição. Se X é a variável aleatória que conta o número de pessoas do sexo feminino escolhidas, e se F(x ) denota a função de distribuição acumulada de X, então F(1,8) é igual a
Uma variável aleatória X tem distribuição normal com média 10 e
variância 5 e uma variável aleatória Y, independente de X, tem
distribuição normal com média 10 e variância 4
A probabilidade de que o valor absoluto da diferença X – Y seja
menor do que 1 é aproximadamente igual a
Uma amostra aleatória de tamanho 100 de uma densidade
exponencial parâmetro λ [ f(x) = λe–λx se x > 0, f(x) = 0, nos
demais casos] foi obtida e mostrou ∑xi = 40.000
O valor observado do estimador não tendencioso de variância
uniformemente mínima de λ é igual a
Para testar H0: μ ≤ 50 versus H1: μ > 50, em que μ é a média
populacional de uma variável N(μ, σ2), uma amostra aleatória de
tamanho 100 foi obtida e mostrou uma média amostral igual a
50,7 com um desvio padrão amostral igual a 5
O p-valor aproximado associado a esses dados e a decisão ao
nível de significância de 5% são, respectivamente,
Suponha que X1 , X2 , ... Xn seja uma amostra aleatória de uma
Poisson com média θ (θ > 0). Suponha ainda que a distribuição
a prioride θ seja uma distribuição gama com parâmetros α e β
(α > 0 e β > 0).
Nesse caso, a distribuição a posteriori de θ dado Xi = xi (i = 1, ..., n) é
Mil famílias responderam a uma pesquisa relacionada com o consumo de três produtos (A, B e (C). A pesquisa revelou o seguinte: 470 famílias consomem o produto A; 420 consomem o produto B; 320 consomem o produto C; 250 consomem ao mesmo tempo os produtos A e B; 150 consomem os produtos A e C; 200 consomem os produtos B e C; e 70 consomem os três produtos. Sorteando-se aleatoriamente a resposta de uma família dentre as entrevistadas, a probabilidade da familiar sorteada consumir um e apenas um dos produtos é
Pedro e João são os oficiais de justiça no plantão do fórum
de determinado município. Em uma diligência distribuída a Pedro,
X é a variável aleatória que representa o sucesso (X = 1) ou
fracasso (X = 0) no cumprimento desse mandado. Analogamente,
Y é a variável aleatória que representa o sucesso (Y = 1) ou
fracasso (Y = 0) de uma diligência do oficial João.
Com base nessa situação hipotética e considerando a soma
S = X + Y, e que P(X = 1) = P(Y = 1) = 0,6 e E(XY) = 0,5, julgue
os itens que se seguem, acerca das variáveis aleatórias X, Y e S.
A variância da soma aleatória S é igual a 0,48.
Um estudo acerca da qualidade dos serviços prestados por um
cartório considerou os indicadores X e Y. A análise de regressão
linear produziu as retas ajustadas (por mínimos quadrados
ordinários) Com relação a esses
indicadores, julgue os itens que se seguem.
Da variação total do indicador Y, 75% são explicados por X.
Considerando a função de densidade conjunta na forma f(x, y) = c,
em que 0 < x < y < 1 e c > 0 é uma constante de normalização,
julgue os seguintes itens.
Com relação à função de densidade condicional, é correto afirmar que
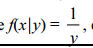
, em que 0 < x < y.
Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido
retirada de uma distribuição exponencial com função de densidade
na forma f(x) = γexp(–γx), em que x > 0 e γ > 0. Com relação a essa
amostra e à inferência estatística, julgue os itens que se seguem.
A função de distribuição acumulada da estatística de ordem X(n) = max{X1, X2, ..., Xn} é P(X(n) ≤ x) = 1 - e-γnx.
Julgue os itens seguintes, relativos às técnicas de amostragem
Considerando que um pesquisador, ao estimar a taxa de
homicídios (R ) em determinada unidade da Federação, tenha
coletado uma amostra de municípios para se obter a estimativa
r da taxa R, que X é o tamanho da população de um dos
municípios e Y é a quantidade de homicídios ali registrados no
ano, então o viés do estimador razão para a taxa de homicídios
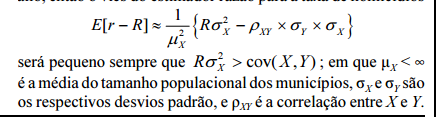
Com referência à estatística computacional, julgue os itens
subsequentes.
Se, em uma simulação de Monte Carlo, for gerado um par de
valores (X, Y) de uma distribuição uniforme em [–1, 1], e, após
m simulações, for calculada a proporção de pares tais que

