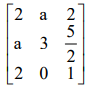Questões de Concurso – Aprova Concursos

Folha de respostas:

1
- a
- b
- c
- d
- e
2
- a
- b
- c
- d
- e
3
- a
- b
- c
- d
- e
4
- a
- b
- c
- d
- e
5
- a
- b
- c
- d
- e
6
- a
- b
- c
- d
- e
7
- a
- b
- c
- d
- e
8
- a
- b
- c
- d
- e
9
- a
- b
- c
- d
10
- a
- b
- c
- d
11
- a
- b
- c
- d
12
- a
- b
- c
- d
13
- a
- b
- c
- d
14
- a
- b
- c
- d
- e
15
- a
- b
- c
- d
- e

6316)

Q649201 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Motorista Escolar,

Das 28 camisetas que Saulo possui, 25% são brancas. Caso ele compre mais 2 camisetas brancas, que porcentagem representará a quantidade de camisetas brancas em relação ao total?

a) 25%
b) 35%
c) 28%
d) 30%
e) 20%

6317)

Q649592 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Agentes Municipais de Trânsito e Transporte,

Um massagista cobra R$ 15,00 pela massagem para clientes com hora marcada e R$ 10,00 sem hora marcada. Ele atende por dia um número fixo de 10 clientes com hora marcada e um número variável x de clientes sem hora marcada. Qual foi o número total de clientes atendidos em um dia em que foram arrecadados R$ 300,00?

a)
15 clientes
b)
10 clientes
c)
25 clientes
d)
30 clientes
e)
20 clientes

6318)

Q651213 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

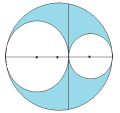
Os dois círculos menores são tangentes externamente entre si e ambos tangenciam internamente o círculo maior. Os centros dos três círculos são colineares e a corda do círculo maior que passa pelo ponto de tangência dos círculos menores mede 40cm. Qual é o valor, em cm², da área sombreada?

a) 150π
b) 175π
c) 100π
d) 200π
e) 125π

6319)

Q651218 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

Uma circunferência tem um diâmetro formado pelos pontos de intersecção da reta 4x + 2y -16 = 0 com os eixos coordenados. Esta circunferência tem a equação dada por

a)
x² -4x + y² -8y = 0
b)
x² +4x + y² +8y = 0
c)
x² -4x + y² +8y -380 = 0
d)
x² +4x +y² +8y -380 = 0
e)
x² -4x +y² -8y -380 = 0

6320)

Q651220 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

Uma reta r é dada pela equação y = 2x e considere o ponto P(2,2). A distância de P à reta r é igual a

6321)

Q651225 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

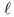
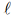
Uma pirâmide de base quadrada tem a mesma altura e o dobro do volume de um cone circular reto. Se é a medida do lado da base da pirâmide e r é a medida do raio da base do cone, então a relação entre e r é igual a

6322)

Q651232 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

Os valores de a para que o determinante da matriz

seja nulo são

a) -2 e -3
b) 2 e 3
c) -5 e 6
d) 5 e -6
e) 1 e 5

6323)

Q651237 - CONPASS - 2017 - Prefeitura de Monteiro - PB - Professor - Matemática

Uma progressão matemática é constituída por 31 termos, cuja soma é 310. O 16º termo desta progressão é

a) 15
b) 20
c) 25
d) 30
e) 10

6324)

Q653048 - EXATUS-PR - 2017 - Prefeitura de Quarto Centenário - PR - Assistente Administrativo,

De uma placa retangular foi diminuído 5 cm no seu comprimento, obtendo assim um quadrado cuja área é 16 cm². Qual era a área desta placa?

a)
36 cm 2 .
b)
38 cm 2 .
c)
40 cm 2 .
d)
42 cm 2 .

6325)

Q584490 - EXCELÊNCIA - 2017 - Prefeitura de Porto Feliz - SP - Professor - Ciências,

a) O limite esquerdo de f(x) quando x tende a 4 é igual a 0;
b) Usando as propriedades dos limites temos lim _x√0 f(x) = lim _x√0 8 - lim _x√0 2x = 8
c) Como f não está definida em 4, lim _x√4 f(x) não existe;
d) Nenhuma das alternativas.

6326)

Q584572 - EXCELÊNCIA - 2017 - Prefeitura de Porto Feliz - SP - Professor - Matemática,

Sabendo que (x — 5)x + 4 = (x — 1)² + 3, o valor de x na equação é:

a)
x = —4;
b)
x = 0;
c)
x = 2;
d)
Nenhuma das alternativas.

6327)

Q584736 - EXCELÊNCIA - 2017 - Prefeitura de Porto Feliz - SP - Professor - Matemática

a) (9, 20, 3) ;
b) (1, -2, -3);
c) (6, 15, 2);
d) Nenhuma das alternativas.

6328)

Q584743 - EXCELÊNCIA - 2017 - Prefeitura de Porto Feliz - SP - Professor - Matemática

Considere o polinômio p(x)=(a-5)x³+6x²+(7.(B)x e assinale a alternativa INCORRETA:

a) Se a ≠ 5 o polinômio p(x) possui grau 3;
b) Se q (x) = p (x) onde q(x)=2x³ + (2.c)x² + 14x temos que a=7,b=2 e c=3 ;
c) Se a = 5 e b = 0, p(x) é um monômio;
d) Nenhuma das alternativas.

6329)

Q623250 - CPCON - 2017 - Prefeitura de Remígio - PB - Agente de Combate a Endemias

Em um sítio há uma criação de bodes e avestruzes e sabe-se que há 660 animais e 2120 pés. Quantos bodes e avestruzes existem no sítio?

a) 300 bodes e 360 avestruzes.
b) 400 bodes e 260 avestruzes.
c) 350 bodes e 310 avestruzes.
d) 360 bodes e 360 avestruzes.
e) 450 bodes e 210 avestruzes.

6330)

Q623255 - CPCON - 2017 - Prefeitura de Remígio - PB - Agente de Combate a Endemias

Uma criança decide quebrar o seu porquinho de moedas e observa que nele existem n moedas de 10 centavos, n + 1 moedas de 25 centavos, 2n moedas de 50 centavos e 2n + 1 moedas de 1 real.

Sabendo que no porquinho tinha 1676,25 reais, quantas moedas existiam no porquinho?

a) 500 moedas.
b) 600 moedas.
c) 300 moedas.
d) 200 moedas.
e) 350 moedas.

Questões de Concurso – Aprova Concursos

Milhares de questões com o conteúdo atualizado para você praticar e chegar ao dia da prova preparado!