Imagine uma figura onde está representado um círculo com um quadrado inscrito. Escolhendo, ao acaso, um ponto do círculo a probabilidade desse ponto pertencer ao quadrado é?
Um super tonel de vinho tem 80% de seu volume ocupado. Retirou-se 200 litros de vinho e seu nível caiu em 20%. Qual o volume total deste tonel?
Seu Inácio, um velho professor de Matemática, lançou um desafio ao neto Pedrinho.
Pedrinho me responda essa:
Aumentando 2 m a medida do comprimento e dobrando a medida da largura de um terreno retangular, o perímetro aumenta 10 m e a área aumenta 42 m². Qual é então, respectivamente, o perímetro e a área desse terreno retangular? Que resposta Pedrinho deveria responder?
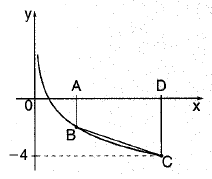
O gráfico seguinte mostra parte do gráfico da função dada por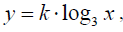 
, em que 
Sabendo que as abscissas de A e D são, respectivamente, 3 e 9, determine o perímetro do trapézio ABCD.
Imagine uma figura onde está representado um círculo com um quadrado inscrito. Escolhendo, ao acaso, um ponto do círculo a probabilidade desse ponto pertencer ao quadrado é?
Considere que a soma dos cubos dos n primeiros números naturais positivos é igual ao quadrado da soma dos mesmos n primeiros números naturais positivos. A soma dos cubos dos 11 primeiros números naturais positivos é um número N, a soma dos algarismos de N vale:
Uma placa controladora, utilizada em robótica, está programada para acionar um efeito sonoro A de 18 em 18 segundos, enquanto uma segunda programação nesta mesma placa aciona um efeito sonoro B de 25 em 25 segundos. Somente quando os efeitos sonoros tocam simultaneamente, uma lâmpada azul acende. Verificando tal programação, percebe-se a lâmpada acender exatamente às 15 horas, 50 minutos e 10 segundos. A partir deste acendimento, qual o horário em que poderá se observar o próximo acendimento da lâmpada azul?
Matemáticos, ligados ao IMPA (Instituto de Matemática Pura e Aplicada) reuniram-se para decidir sobre duas abordagens que serão implementadas na área de pesquisas econômicas para o próximo ano: Mercados Incompletos e a Teoria do Capital. Dos 116 matemáticos presentes, 88 foram a favor da implementação da abordagem em Mercados Incompletos, 84 foram a favor da implementação da abordagem da Teoria do Capital e 63 estavam a favor da implementação das duas abordagens. Neste caso, o número de Matemáticos presentes, que não foram a favor de nenhuma das abordagens foi de:
O baralho é um conjunto de 52 cartas divididas em 4 naipes diferentes (copas e ouro – que são as cartas de cor vermelha e paus e espada – que são as cartas de cor preta). Cada uma das 13 cartas de cada naipe recebe um valor que varia de 2 (Dois) ao A (As), neste caso, tem-se para cada naipe os valores 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K e A.
No jogo de Poker, a segunda jogada mais forte é o “Straight Flush", que são 5 cartas seguidas do mesmo naipe desde que não seja do 10 até ao As, pois, neste caso, seria a jogada mais forte, que é o “Royal Straight Flush". Lembrando que a carta As é a única do baralho que pode variar a sua posição, ou seja, pode vir após o Rei (K), ou antes do dois (2).
Em um baralho normal de 52 cartas, o número de combinações para o “Royal Straight Flush" é de 4 possibilidades. Determine, neste caso, quantas possibilidades há em um baralho normal de 52 cartas para a segunda jogada mais forte do Poker, que é o “Straight Flush"?
Fonte da imagem: http://www.materiaincognita.com.br">www.materiaincognita.com.br
Uma operação policial será realizada com uma equipe de seis agentes, que têm prenomes distintos, entre eles André, Bruno e Caio. Um agente será o coordenador da operação e outro, o assistente deste; ambos ficarão na base móvel de operações nas proximidades do local de realização da operação. Nessa operação, um agente se infiltrará, disfarçado, entre os suspeitos, em reunião por estes marcada em uma casa noturna, e outros três agentes, também disfarçados, entrarão na casa noturna para prestar apoio ao infiltrado, caso seja necessário.
A respeito dessa situação hipotética, julgue o item seguinte.
A quantidade de maneiras distintas de formar a equipe, de modo que André, Bruno e Caio sejam os agentes que prestarão apoio ao infiltrado, é inferior a 10.
Dadas as afirmativas,
I. Se x e y são dois inteiros pares, então a diferença x – y é um inteiro par.
II. Se x é um inteiro par e y é um inteiro ímpar, então o produto x2y2 é um inteiro par.
III. Se x e y são dois inteiros ímpares, então a soma x + y é um inteiro ímpar.
verifica-se que está(ão) correta(s)
Do texto, infere-se que milha é unidade de
Pedro é servidor de uma autarquia municipal, no ano de 2016 recebeu um reajuste salarial de 4% no mês de maio e mais 4% no mês de novembro. Se o salário de Pedro em abril de 2016 era de 1.000,00, quanto passou a receber em dezembro de 2016?
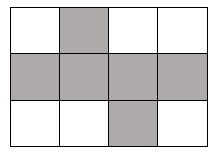
A figura abaixo representa uma folha de papel retangular, onde estão destacados 6 quadrados. Com a parte destacada dessa folha, pode-se montar um cubo. Se a área da folha é 432 cm², qual o volume desse cubo, em cm³?
Sendo A = {-1, 0, 1, 2, 3, 5}, B = {2, 4, 6, 8} e C = {-2, 1, 3}, podemos determinar (A – B) UC como sendo o conjunto:
