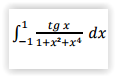Carlos possui um cofre com N moedas de R$ 0,50 e de R$ 1,00. Ele retirou do cofre 25 moedas do R$ 0,50, o número de moedas restantes é tal que o número de moedas de R$ 1,00 é quatro vezes o número de moedas de R$ 0,50. Num segundo momento, Carlos retira 37 moedas de R$ 1,00 do cofre e o número de moedas restantes é tal que o número de moedas de R$ 0,50 é a terça parte das moedas de R$ 1,00. Quantas moedas restaram no cofre?
Seja z um número complexo tal que 2
z+z = 64 e o número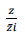 
tem argumento 
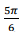. O número z tem módulo igual a:
O resultado da multiplicação de dois números (X e Y) resultam em um numero impar. Com essa informação assinale a alternativa CORRETA que caracterize os números X e Y:
Um produto tem na sua composição diferentes matérias-primas (X, Y e Z) e o quadro abaixo apresenta os seus respectivos preços (em unidades monetárias) e quantidades nas épocas 0 (passado) e 1 (atual).
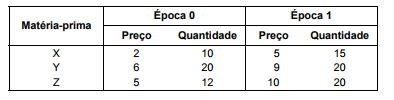
Utilizando as informações deste quadro, tem-se que os correspondentes índice de preços de Laspeyres e o índice de quantidades de Paasche, considerando as épocas 0 e 1, são, respectivamente,
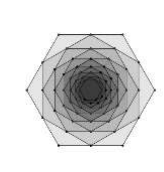
Dado um hexágono regular H1, cujo lado tem comprimento 4 cm, considere a sequência infinita de hexágonos regulares {H1, H2, H3, ...} onde cada hexágono é obtido unindo-se os pontos médios dos lados do hexágono anterior. Sabendo que a medida do perímetro do hexágono H2 é 12√3 cm, o limite da soma das áreas dos infinitos hexágonos da sequência é:
Uma pizza foi dividida em 12 pedaços logo 1/4 da pizza corresponde a:
Ao querer comprar um troféu que custava 258 reais um grupo de três amigos conseguiu um desconto de 18 reais. Sabendo que a compra foi realizada, o valor pago foi dividido igualmente entre os três, quanto cada um pagou?
José foi até uma loja de departamentos para comprar um aparelho de televisão. Por realizar pagamento em dinheiro, José recebeu desconto de 10%, e o valor final do equipamento foi R$ 1.763,55 (mil setecentos e sessenta e três reais e cinquenta e cinco centavos). Maria comprou o mesmo equipamento, mas preferiu dividir o valor da televisão em 10 vezes de R$ 235,14 (duzentos e trinta e cinco reais e quatorze centavos), um acréscimo de 20%. Use as informações acima e calcule o valor do equipamento sem nenhum desconto ou acréscimo.
Considerando a função afim f de R em R dada por f(x)=3x-7 , podemos afirmar que:
Analise as afirmativas sobre a função f: {-1,0,1,2) —> R, definida por f (x) = (x + 2)2 —(x — 1)2 e assinale a alternativa CORRETA:
I- A função é decrescente.
II- A imagem da função é dada pelo conjunto Im = {-3, 3, 9,15).
III- O valor de f (0) = 0
A integral
resulta em:
Os Parâmetros Curriculares Nacionais para a área de Matemática no ensino fundamental estão pautados por princípios decorrentes de estudos, pesquisas, práticas e debates desenvolvidos nos últimos anos. Sobre tais princípios assinale a alternativa INCORRETA:
O Brasil possui 200 milhões de habitantes. Um quarto é beneficiado pelo Programa Bolsa Família. Um quinto dos beneficiados está distribuído entre os quatro estados da região Sudeste e dois quintos entre os nove estados da região Nordeste. O número de habitantes da região Sudeste que é beneficiado pelo Bolsa Família é de:
O preço de um caminhão, P(t), desvaloriza em função do tempo de uso t, dados em anos, por uma função do tipo exponencial dada por P(t )=y . xt , sendo x e y constantes positivas. Considere que o preço do caminhão novo (t=0) seja R$ 250 000,00 e que será R$ 160 000,00 depois de dois anos de uso. Quanto será o preço do caminhão depois de cinco anos de uso?
A figura a seguir representa um cubo no qual as faces
laterais possuem três furos, ocupados ou não, em vários
formatos geométricos. Cada uma das seis faces da caixa é
um quadrado com três furos, e as faces opostas são iguais.
Nessas condições, quantos furos da caixa têm o formato de
um quadrilátero?
