A planificação a seguir é referente à lateral de um cone reto, com todas as medidas dadas em centímetros.
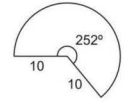
Dessa forma, o volume deste cone, em cm3, é:
Um automóvel tem seu consumo de combustível para percorrer 100 km estimado pela função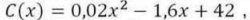 
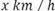
com velocidade de 
. Sendo assim, qual deve ser a velocidade para que se tenha um consumo mínimo de combustível?
Considere a matriz
e ainda que det M é o determinante da matriz M. Dessa forma, pode-se afirmar que a equação det M = 2 tem raízes cuja soma é igual a:
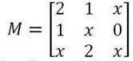
Uma embalagem de papelão em formato de paralelepípedo foi construída de forma que suas arestas são diretamente proporcionais a 3, 4 e 5 e a soma dessas medidas é igual a 120 cm. Então a medida de sua área total, em cm2, é igual a:
Um artesão constrói peças em formato cilíndrico sempre com medidas: altura 20 em e raio da base 10 cm. Sabendo que ele pinta todas as peças e que uma lata de tinta tem um rendimento de 3000 cm2, pode-se afirmar que para 12 peças cilíndricas será necessário um número de latas igual a:
Em uma Progressão Geométrica o terceiro termo é 36 e a razão é igual a 
. O primeiro termo dessa sequência é:
Um posto de saúde recebeu 15 litros de determinada vacina distribuídos em ampolas de 40 cm3 cada uma. A quantidade de ampolas de vacina que esse posto recebeu foi:
Em um pequeno aeroporto de uma cidade, o controle de tráfego aéreo é responsável por organizar os tempos de pousos e decolagens a fim de que não haja convergência entre esses horários. Ao organizar os tempos, caso ocorra a convergência nesse horário comum, não haverá pouso ou decolagem de nenhuma aeronave. Com a tabela de pousos pronta, os funcionários do controle de tráfego aéreo tinham em mãos o horário da decolagem das aeronaves de três diferentes empresas. Na empresa A, as aeronaves decolam de 45 em 45 minutos. Na empresa B, as aeronaves decolam de 60 em 60 minutos e, na empresa C, de 75 em 75 minutos.
Se o primeiro horário, verificado pelos controladores, em que as três empresas realizarão a decolagem juntas é à 1:00 h, então o próximo horário em que isto ocorrerá novamente é às:
Rafaela é dona de uma loja e no mês de dezembro de 2017 remarcou seus preços com dois descontos sucessivos de 10% e um desconto de 20%.
O desconto equivalente a esses três descontos foi:
Um grupo com 12 agentes de manutenção consomem em seis dias 108 pães. Quantos pães serão necessários para quatro dias se três deles estiverem de férias?
Um garoto economizou sua mesada durante alguns meses para comprar alguns itens em uma feira de jogos. Durante a feira, se ele comprasse três cartuchos de um jogo e duas miniaturas de seu herói favorito faltariam R$ 31,00 para pagar a compra. Por outro lado, se ele comprasse dois cartuchos do jogo e três miniaturas sobrariam R$ 16,00. Considerando que o valor de um cartucho e de uma miniatura totaliza R$ 283,00, o valor que ele economizou para comprar esses itens na feira foi de
A partir do texto e do diagrama acima, assinale a alternativa correta.
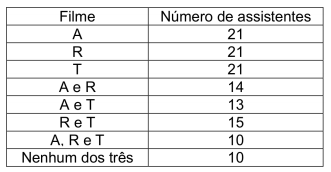
Os dados de uma pesquisa realizada com um grupo de assistentes sobre três filmes (A, R e T) foram tabelados a seguir:
De acordo com os dados anteriores, o número de assistentes que não optaram pelos filmes R ou T é:
A respeito de proporções e porcentagens, julgue o item seguinte.
Suponha-se que, em determinado Conselho Regional de Odontologia (CRO), haja 1.540 processos, que deverão ser analisados pelos advogados Mário, Natanael e Sandra. Houve uma divisão desses processos entre os três e sabe-se que, a cada 4 processos recebidos por Mário, Natanael recebeu 3 e que, a cada 6 processos recebidos por Mário, Sandra recebeu 7. Nesse caso, Natanael e Sandra receberam, juntos, mais de 1.100 processos.
A respeito de operações com números e conjuntos, julgue o item.
Dos alunos que frequentam um curso preparatório para concursos públicos, sabe-se que 58 leem o jornal X, 28 leem os jornais X e Y, 120 leem apenas um desses jornais e 69 não leem o jornal Y. Sabendo que existem candidatos que não leem nenhum dos dois jornais, é correto afirmar que, nesse curso, há mais de 180 alunos.
