A produtividade do magistrado (Z) é um indicador que
permite medir a celeridade dos processos judiciais. Ela é definida
como uma razão na forma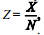
em que X representa o total anual
de processos julgados pelos magistrados de certo tribunal e N, uma
constante, representa o total de magistrados existentes nesse
tribunal. Embora X seja uma variável aleatória discreta, ela pode ser
aproximada por uma distribuição normal com média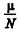 
e desvio padrão 
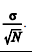Com base nessa situação hipotética, julgue os itens a seguir.
A produtividade do magistrado é uma variável aleatória que
segue, aproximadamente, uma distribuição normal com média
e desvio padrão .
Com o propósito de produzir inferências acerca da
proporção populacional (p) de pessoas satisfeitas com determinado
serviço oferecido pelo judiciário brasileiro, foi considerada uma
pequena amostra de 30 pessoas, tendo cada uma de responder 1,
para o caso de estar satisfeita, ou 0, para o caso de não estar
satisfeita. Os dados da amostra estão registrados a seguir.
0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1
Com base nessas informações, julgue os itens seguintes.
Caso o p–valor do teste H0: p = 0,5 versus H1: p … 0,5 seja igual
a 0,0295, então, se a hipótese alternativa fosse alterada para
H1: p < 0,5, o teste seria significativo ao nível de significância
de 2%.
Segundo notícia veiculada recentemente, em rede nacional,
os processos do judiciário estão demorando mais que o razoável
porque os juízes têm de analisar, em média, 3 mil processos por
ano. Para verificar o fato, um analista coletou a quantidade de
processos de uma amostra de 10 juízes, estando os resultados
dispostos a seguir (em mil processos por ano).
2 5 4 3 2 2 3 3,5 2,5 5
Com base nessas informações e considerando que μ representa a
média populacional por juiz, julgue os itens subsequentes.
A estatística do teste para se testar se H0: μ = 3 mil possui 8
graus de liberdade, dada a necessidade de se estimarem a
média e o desvio–padrão e sabendo que os dados seguem uma
distribuição normal.
Para verificar se a escolaridade dos servidores de
determinado tribunal estaria relacionada à eficiência no atendimento
ao público, um analista pesquisou alguns servidores, dispondo as
informações obtidas na tabela a seguir.
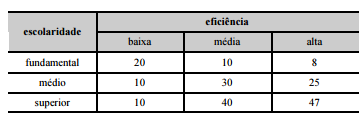
Com base nessas informações e considerando que a escolaridade de
cada servidor entrevistado, apresentada na tabela, corresponda à
maior escolaridade que possui, julgue os itens seguintes.
Para verificar se as variáveis estão associadas, pode–se utilizar
o teste qui–quadrado com 4 graus de liberdade.
Para verificar se a escolaridade dos servidores de
determinado tribunal estaria relacionada à eficiência no atendimento
ao público, um analista pesquisou alguns servidores, dispondo as
informações obtidas na tabela a seguir.
Com base nessas informações e considerando que a escolaridade de
cada servidor entrevistado, apresentada na tabela, corresponda à
maior escolaridade que possui, julgue os itens seguintes.
O estudo em questão insere–se entre as restrições para o uso do
teste qui–quadrado, visto que todos os valores esperados são
maiores que 5.
O administrador de uma organização, antes de promover
um processo de treinamento de pessoal, fez um treinamento piloto
com 10 empregados para verificar a eficácia da metodologia
aplicada no treinamento. A tabela a seguir mostra a quantidade de
processos resolvidos por cada um desses 10 empregados,
numerados de 1 a 10, no mês anterior ao treinamento piloto e no
mês seguinte.
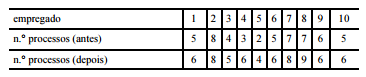
Considerando as informações acima e que os dados da tabela
seguem uma distribuição normal, julgue os itens subsequentes.
O teste dos sinais tende a ser mais liberal do que o teste a ser
aplicado aos dados, uma vez que a magnitude do ganho da
metodologia empregada não é considerada.
Com relação aos modelos de regressão, julgue os itens
subsecutivos.
O estimador de mínimos quadrados para um modelo de
regressão linear simples para uma variável resposta IID, é não
viciado e possui mínima variância.
Julgue os próximos itens, referentes à qualidade de ajuste de um
modelo de regressão.
Considere que em uma tabela de ANOVA para ajuste de um
modelo de regressão a esperança da soma de quadrados do
resíduo é igual a 15 vezes a variância da variável resposta.
Nesse caso, o tamanho amostral é inferior a 20 unidades.
Com relação à análise de regressão linear, julgue os itens que se
seguem.
Em um modelo de regressão linear, se a variável explicativa e
a variável resposta não se correlacionam, o coeficiente de
determinação seria próximo de 0. Além disso, se o coeficiente
de determinação fosse próximo de 0, as variáveis explicativa
e resposta seriam independentes.
Com relação à análise de regressão linear, julgue os itens que se
seguem.
Em um modelo linear simples, se a correlação entre os quantis
do resíduo padronizado e uma amostra aleatória da normal
padrão for alta, o modelo não terá intercepto.
Sejam X o número de contratos realizados, e Y o número de contratos cancelados em uma determinada agência, por dia. A distribuição conjunta de X e Y é dada por
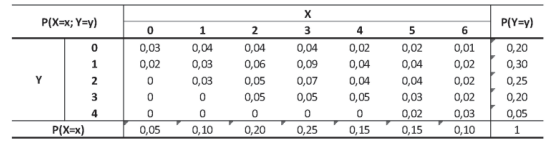
Dado que pelo menos quatro contratos novos foram fechados, a probabilidade de que três contratos sejam cancelados no mesmo dia é:
Relativamente à análise de Séries Temporais considere:
I. A análise espectral de séries temporais é fundamental em áreas onde o interesse básico é a periodicidade dos dados.
II. Se Zt é um processo de ruído branco de média zero e variância 1, a sua função de densidade espectral é dada por
III. Um modelo ARIMA(1,1,1) é um modelo com um componente autorregressivo, um componente sazonal e um componente de médias móveis.
IV. As funções de autocorrelação e autocorrelação parcial de um modelo ARMA são primordiais para a identificação do modelo.
Está correto o que consta em
Relativamente à Análise Multivariada, considere as seguintes afirmações:
I. Seja X uma variável aleatória normal univariada com média µ1 e variância σ
12 tem distribuição normal univariada com média μ
2 e variância σ22. Nessas condições, o vetor (X Y) tem distribuição normal bivariada.
II. Se ∑ é a matriz de covariâncias de um determinado vetor aleatório, então ∑ é uma matriz positiva definida.
III. A variância total de um vetor aleatório é dada pelo traço de sua matriz de covariâncias.
III. A variância total de um vetor aleatório é dada pelo traço de sua matriz de covariâncias.
IV. Se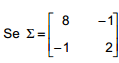 
é a matriz de covariâncias do vetor aleatório X de dimensão (2X1), então a matriz de correlações de X é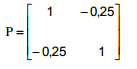 
Está correto o que consta APENAS em
Suponha que o número de consultas a um banco de dados, disponível em um Tribunal Regional do Trabalho, tenha distribuição
de Poisson com taxa média de 4 consultas por hora. A probabilidade de, na próxima meia hora, ocorrer mais de uma consulta,
sabendo−se que na próxima meia hora é certa a ocorrência de, pelo menos, uma consulta é
Dados: e−2 = 0,135
e−4 = 0,018
