Um lote é formado por 10 artigos bons e 5 com pequenos defeitos. Uma amostra aleatória, sem reposição, de 3 artigos é selecionada do lote. Se a amostra só tiver artigos bons, o lote é vendido por R$ 455,00; se a amostra tiver 2 artigos bons, o lote é vendido por R$ 273,00 e se a amostra tiver menos do que 2 artigos bons, o lote é vendido por R$ 182,00. Nessas condições o preço médio de venda do lote é, em reais, igual a
Sejam X e Y duas variáveis aleatórias independentes. Sabe−se que X tem distribuição binomial com parâmetros n = 2 e p = 0,3 e que Y tem distribuição uniforme discreta no intervalo, fechado, de números inteiros [2, 4]. Nessas condições P(X + Y ≤ 4) é igual a
Considere a tabela de frequências absolutas abaixo, correspondente aos salários dos 80 funcionários lotados em um órgão
público.
O valor da média aritmética dos salários foi obtido considerando que todos os valores incluídos em um certo intervalo de classe
são coincidentes com o ponto médio deste intervalo. O valor da mediana foi obtido pelo método da interpolação linear. A
porcentagem que o valor da mediana representa do valor da média aritmética dos salários é, em %, igual a
Uma variável contínua X apresenta uma média igual a 50. Pelo Teorema de Tchebyshev, a probabilidade de X não pertencer ao intervalo (10, 90) é no máximo 25%. O resultado da divisão da variância de X pelo quadrado da média de X é
Dois grupos são formados, respectivamente, de amostras aleatórias independentes provenientes de duas populações constituídas
de escores. Pretende−se aplicar o teste da mediana, cujo objetivo é verificar se as medianas dos grupos são iguais. Sobre
este teste, considere as seguintes afirmações:
I. Não poderá ser aplicado caso sejam desconhecidas as distribuições das populações dos grupos.
II. Poderá ser aplicado mesmo que os tamanhos dos grupos sejam diferentes.
III. Não poderá ser aplicado caso ocorra, pelo menos, um empate entre os dados dos dois grupos.
IV. Poderá ser aplicado se combinando os escores dos dois grupos, verifica−se que o valor da mediana do conjunto formado
não pertence a qualquer um dos grupos.
Está correto o que consta APENAS em
Um fabricante de pneus afirma que seu produto pode rodar, em média, 60.000 km. Para averiguar tal afirmação, um pesquisador seleciona 49 pneus e obtém uma média de 58.000 km e um desvio padrão de 7.000 km.
Se as hipóteses a serem testadas são H₀ : μ = 60.000 H₁ : μ < 60.000, conclui-se que o p-valor é
Em um teste de hipóteses bilateral, com nível de significância α, cujas estatísticas de teste calculadas e tabeladas são designadas por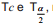 
respectivamente, pode-se afirmar que:
Os modelos abaixo foram propostos e ajustados a 30 observações de quatro variáveis de interesse:
O valor da estatística F usada para testar se os parâmetros β3 e β4 são ambos nulos é
Considere as informações a seguir para responder às questões de n os 57 a 60.
Considere o problema abaixo de Programação Linear: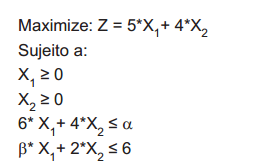 
Considere que β= 1.
Qual o valor mínimo que α pode assumir para que a base ótima para o problema de programação linear apresentado permaneça a mesma encontrada quando α= 24?
Em um teste de hipótese estatístico sobre um parâmetro, define-se o poder do teste como a
Considere as informações a seguir para responder às questões de n os 57 e 58.
Uma empresa decide investir a quantia de 500 mil reais na construção de uma pequena central hidrelétrica. Ao analisar a viabilidade do empreendimento, ela prevê que, ao longo dos próximos quatro anos, terá receitas com a comercialização da energia e despesas de operação e manutenção, conforme a Tabela apresentada a seguir.
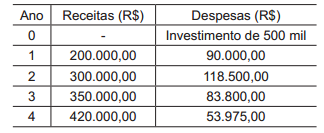
Considere que o investimento foi realizado no ano zero, e que a empresa utiliza uma taxa de juros de 10% ao ano.
Pelo critério do pay-back descontado, o tempo t, em anos, que se leva para recuperar o investimento inicial é tal que
Em um treinamento destinado aos recém-formados de uma faculdade é realizado um levantamento com relação às idades (em
anos) de seus participantes e obteve-se a seguinte tabela:
Sendo Me, Md, e Mo os valores da média aritmética (em anos por participante), da mediana e da moda, respectivamente,
observa-se, com relação à tabela, que
Seja X uma população {X1, X2, X3, ... , X100 } formada por 100 números estritamente positivos com um desvio padrão igual a 4 e
com a soma dos quadrados de todos estes 100 números igual a 41.600. Seja Y uma outra população { Y1, Y2, Y3, ... , Y50 }
formada por 50 números também estritamente positivos com uma média igual a da população anterior e com a soma dos
quadrados de todos estes 50 números igual a 20.200. Os coeficientes de variação de X e de Y
As variáveis aleatórias X e Y representam a altura (em centímetros) dos habitantes de uma cidade e o peso (em quilos) dos
habitantes de uma outra cidade, respectivamente. Considera-se que as correspondentes populações de X e Y são normalmente
distribuídas e de tamanho infinito. Uma amostra aleatória de tamanho 100 da população de X forneceu um intervalo de
confiança, ao nível de confiança de 88%, para a média (μx), em cm, igual a [156,1 ; 163,9], sabendo-se que a variância
populacional de X é igual a 625 cm². Uma amostra aleatória de tamanho 400 da população de Y forneceu um intervalo de
confiança, ao nível de confiança de 88%, para a média (μy), em kg, igual a [68,83 ; 71,17]. A variância populacional de Y, em
kg² , é igual a
Atenção: Para responder às questões de números 36 e 37, considere a informação abaixo.
A equação da reta y = a + bx foi obtida pelo método dos mínimos quadrados, com base em 10 observações (xi , yi ), i = 1, 2, 3, ...,10, em que foi dotado o modelo linear y i = α + βxi + εi . As estimativas de α e β são respectivamente a e b, i corresponde a i-ésima observação e εi é o erro aleatório com as correspondentes hipóteses do modelo linear simples. Sabe-se que a reta determinada pela equação acima passa pelos pontos ( 20 , 40 ) e ( 100 , 20 ).
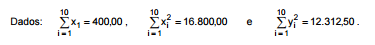
A estimativa da variância σ² do modelo teórico é igual a
