INSTRUÇÃO: Com base na tabela a seguir, que se refere às distâncias percorridas (em km) pelos cem veículos do DETRAN, na última semana do ano de 2014, responda às questões 95 e 96.
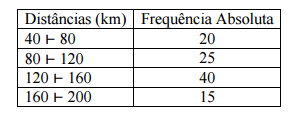
Segundo a tabela dada, o valor da moda será:
Dados os valores de uma variável: 5, 10, 15, 20, 25, as
variâncias amostral e populacional são, respectivamente,
Uma equipe de pesquisadores a serviço da prefeitura de
uma cidade está planejando um estudo junto à população
para verificar a relação entre renda e prática de esportes.
Com relação à amostra a ser colhida, o plano prevê sondagens
com 30 praticantes de futebol, 30 praticantes de
natação e 30 praticantes de corrida, todos selecionados
aleatoriamente entre os praticantes de cada modalidade.
Uma amostra assim obtida é denominada
Somando–se os valores absolutos dos desvios individuais
dos salários tomados em relação à média, encontra–se o
valor de
Para avaliar o tempo médio de viagem entre o ponto
inicial e o ponto final de uma linha de ônibus, retira–se
uma amostra de 36 observações (viagens), encontrando–
–se, para essa amostra, o tempo médio de 50 minutos
e o desvio padrão de 6 minutos, com distribuição normal.
Considerando–se um intervalo de confiança de 95%
para o tempo médio populacional, é correto afirmar que o
valor mais próximo para limite inferior desse intervalo é
o tempo de
Para estimar a média e a variância utilizando estimadores
de momentos, dada uma amostra de n elementos
de uma distribuição normal, N(μ ; σ2), a partir de
uma amostra de n elementos extraídos da população,
x = (x1; x2;...xn), assinale a alternativa que contém a
afirmação verdadeira.
Ao se montar a tabela ANOVA para esse caso, obtiveram–se
os seguintes valores:
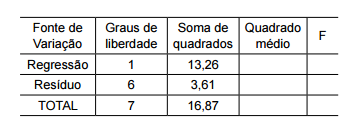
Ao complementar a tabela e calcular o valor de F, encontra–se
o valor aproximado de
Ao construir a ANOVA, é necessário preencher a tabela
a seguir:
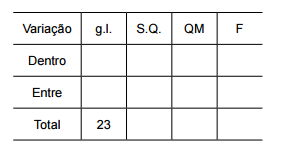
Nesse caso, o valor de F é, aproximadamente,
Considere as seguintes afirmações:
I. O histograma é um gráfico apropriado para verificar o grau de associação linear entre duas variáveis aleatórias
quantitativas.
II. Se duas variáveis X e Y apresentam correlação linear inversa, o coeficiente de correlação linear entre elas será um
número negativo menor do que –1
III. As amostras I e II dadas abaixo possuem a mesma variância amostral igual a 10
Amostra I: 1 3 5 7 9
Amostra II: 11 13 15 17 19
IV. A distribuição t de Student é apropriada para se fazer inferências sobre a média de uma população quando o desvio
padrão dessa população é desconhecido.
Está correto o que se afirma APENAS em
Analisando a quantidade diária de processos autuados em uma repartição pública, durante um período, obteve-se o seguinte
gráfico em que as colunas representam o número de dias em que foram autuadas as respectivas quantidades de processos
constantes no eixo horizontal.
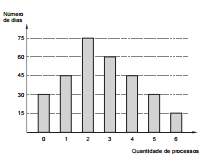
A soma dos valores respectivos da mediana e da moda supera o valor da média aritmética (quantidade de processos autuados
por dia) em
Utilizando o método dos momentos, deseja-se obter uma estimativa do parâmetro p da distribuição geométrica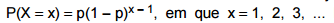 
Para isto, observou-se em 6 experiências quando determinado evento com
probabilidade p ocorreu pela primeira vez. A tabela abaixo apresenta o resultado destas observações:
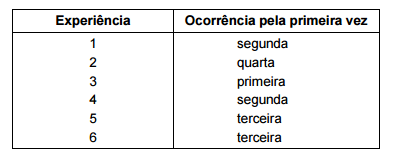
O valor desta estimativa, com base nestas experiências, é, em %, de
Um pesquisador desenvolve um estudo com uma população normal, considerada de tamanho infinito e desvio padrão populacional
igual a 65. Sendo μ a média da população, deseja executar o teste H0: μ = 70 (hipótese nula) contra H1: μ > 70 (hipótese
alternativa). Para isto, utiliza uma amostra aleatória de tamanho 400 com um nível de significância de 5%, considerando que na
curva normal padrão (Z ) as probabilidades P(Z > 1,64) = 0,050 e P(Z > 1,96) = 0,025. O pesquisador encontrou um valor para a
média amostra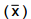 
sabendo-se que este valor é o maior valor tal que H0 não é rejeitada. O valor de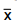 
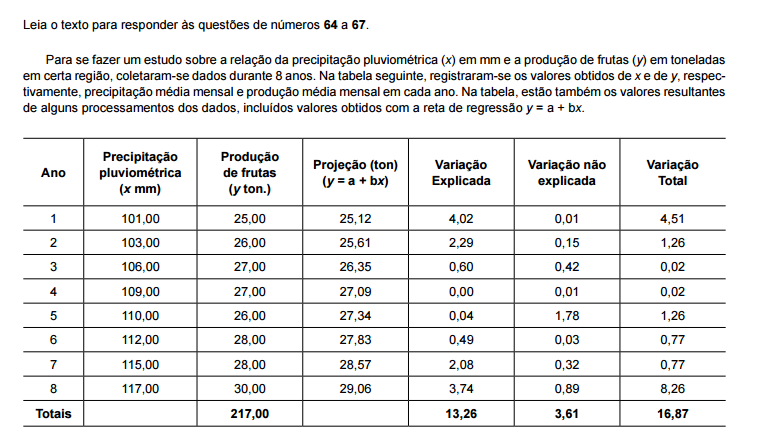
Atenção: Para responder às questões de números 38 a 40, considere o modelo linear , Yi = α + β + ε sendo i a i-ésima observação, Yi a variável dependente na observação i, X a variável explicativa na observação i e i i ε o erro aleatório com as respectivas hipóteses para a regressão linear simples. Os parâmetros α e β são desconhecidos e suas estimativas (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados e com base em 20 pares de observações ( X , i Y ), i = 1, 2, ... , 20. Sabe-se que os pontos (10 ; 9,8) e (40 ; 33,8) pertencem à reta de equação Y i = a + bX.
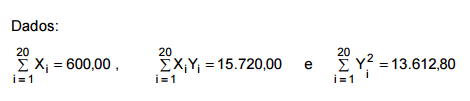
O valor de S, em que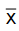 
é o valor médio dos 20 valores observados para X tal que
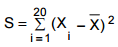é igual a
