Atenção: Para responder às questões de números 58 a 60 use, dentre as informações dadas abaixo, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:
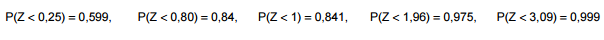
Considere W=(X/Y) uma variável aleatória com distribuição normal multivariada com vetor de médias µ = (2/3) e matriz de covariâncias
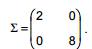Seja a variável aleatória U = 2X - Y. A probabilidade de U assumir um valor entre 2 e 5, denotada por P(2 < U < 5) é
igual a
Uma variável aleatória X contínua tem função de densidade de
probabilidade dada por f(x) = e–x, se x > 0, f(x) = 0, nos demais
casos.
A média de X é igual a
Suponha que a componente sistemática de um erro de medição
seja uma variável aleatória X com distribuição uniforme no
intervalo [–2, 4].
A média e a variância de X valem, respectivamente,
Se X é um variável aleatória com função de distribuição
acumulada contínua F(x), então a variável aleatória Y = F( X ) tem
distribuição
Se X1 , X2 , .., Xn denota uma amostra aleatória de tamanho n de
uma distribuição N (μ, σ2), então os estimadores de máxima
verossimilhança de μ e σ2
são respectivamente:
Para se testar a significância de uma regressão linear múltipla,
dados foram observados e a seguinte tabela (incompleta) foi
obtida:
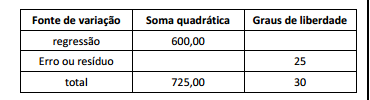
O valor da estatística F é igual a
Para uma amostra aleatória de tamanho 5, observou-se
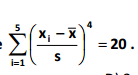
A medida de curtose para esses dados é
Seja
O coeficiente de variação de X é
O modelo de regressão linear simples Yi = β 0 + β1Xi + ▱i foi ajustado a um conjunto de dados. Nesse modelo, os erros são
variáveis aleatórias independentes com distribuição normal e variância constante e os parâmetros foram estimados
pelo método de mínimos quadrados. Alguns resultados são apresentados a seguir. (Considere: coeficiente de correlação
amostral = 0,94)
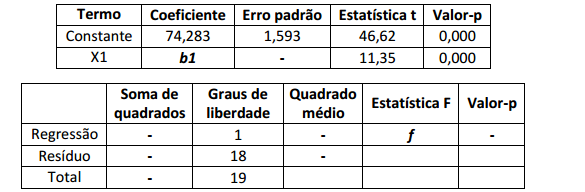
Considerando os resultados apresentados, é INCORRETO afirmar que o(a)
O responsável pelo controle de qualidade de uma indústria pretende construir um gráfico de controle para a força de
resistência de uma peça metálica. Sabendo-se que a força de resistência tenha distribuição normal, 30 amostras de
tamanho n = 5 foram coletadas durante um período, obtendo-se
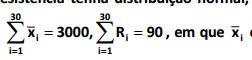
é a média amostral
da i-ésima amostra e Ri é a i-ésima amplitude amostral da i-ésima amostra. Para o gráfico de controle da média, o
limite inferior de controle três-sigma e o limite inferior de controle de probabilidade 0,001 são, respectivamente,
A maioria dos modelos de previsão tem base na ideia de que observações passadas contêm informações sobre o padrão de comportamento da série temporal. O propósito dos métodos é distinguir o padrão de qualquer ruído que possa estar contido nas observações e então usar esse padrão para prever valores futuros das série. Com base nessas informações, assinale a alternativa que apresenta uma classe de métodos de previsão, que tenta tratar as causas das flutuações em séries de tempo.
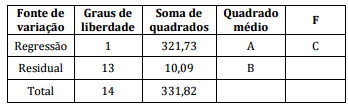
Considerando a tabela de ANOVA apresentada, que é para
um determinado modelo de regressão, assinale a
alternativa que corresponde, respectivamente, aos valores
de A, B e C:
Dada a amostra:
I) 20, 30, 40, 50, 60
Com base nos dados apresentados, assinale a alternativa
que indica a média, a variância e o desvio-padrão da
amostra.
Assinale a alternativa que apresenta a divisão dos estados em um processo de Markov.
Uma pesquisa em uma determinada universidade resultou
na seguinte tabela de dados (x,y):
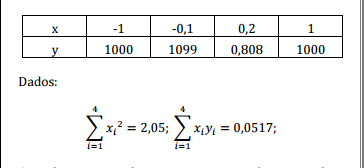
Com base nas informações apresentadas, assinale a
alternativa que indica a equação da reta, construída
através do método dos mínimos quadrados que melhor se
ajusta aos pontos.
