A comissão de erradicação do trabalho infantil de um determinado Tribunal Regional do Trabalho analisa, por meio de seu canal
de denúncias, casos de desrespeito à legislação que regula o trabalho de menores de 18 anos. Suponha que a variável X, que
representa o número de denúncias mensais que são recebidas, tem distribuição de Poisson com média 9. Nessas condições, a
probabilidade de serem recebidas 2 ou 3 denúncias em um período de 10 dias é igual a
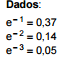
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
-------------------
Instrução: O enunciado a seguir refere-se às questões de números 49 a 51. Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
O valor de K, em anos, tal que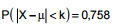 
é igual a
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
-------------------
Instrução: O enunciado a seguir refere-se às questões de números 49 a 51. Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de 16 trabalhadores será selecionada e sejam X1, X2, ...X16 as idades observadas e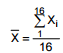 
a média desta amostra. Sabendo-se que a probabilidade de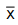 
ser superior a 30 anos é igual a 0,919, o valor de μ,
em anos, é igual a
Seja X uma variável aleatória com função densidade de probabilidade dada por:
onde k é uma constate real que torna f(x) uma função densidade de probabilidade.
Nessas condições, a função densidade de probabilidade da variável aleatória Y = 3X + 4, no intervalo 4 < y < 10 é dada por
Em dado relatório de avaliação da qualidade do transporte aéreo considerou-se a relação entre o nível de estresse de
controladores de tráfego aéreo e a ocorrência de incidentes
aeronáuticos. Para o estudo, foram selecionados ao acaso 251
controladores de tráfego aéreo, que foram separados em dois
grupos, de acordo com seus níveis de estresse. A tabela a seguir
mostra a quantidade de incidentes registrados dentro de cada grupo.
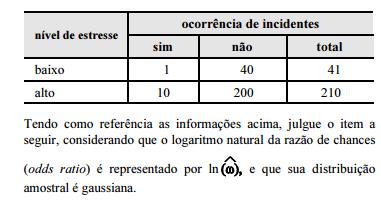
O erro padrão de 
é inferior a 1
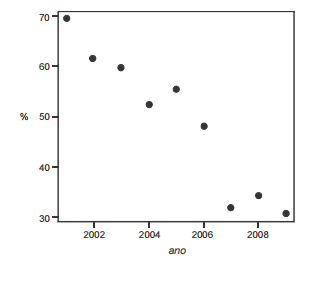
Dado que a participação dos presidiários em cursos de qualificação profissional é um aspecto importante para a reintegração do egresso do sistema prisional à sociedade, foram realizados levantamentos estatísticos, nos anos de 2001 a 2009, a respeito do valor da educação e do trabalho em ambientes prisionais. Cada um desses levantamentos, cujos resultados são apresentados no gráfico, produziu uma estimativa anual do percentual P de indivíduos que participaram de um curso de qualificação profissional de curta duração, mas que não receberam o diploma por motivos diversos. Em 2001, 69,4% dos presidiários que participaram de um curso de qualificação profissional não receberam o diploma. No ano seguinte, 2002, esse percentual foi reduzido para 61,5%, caindo, em 2009, para 30,9%. A partir das informações e do gráfico apresentados, julgue os itens que se seguem.
Caso a quantidade total de presidiários participantes de um curso de qualificação profissional em 2001 seja igual a N, e esse total em 2002 seja igual a 2N, a estimativa do percentual P de indivíduos que participaram de um curso de qualificação profissional de curta duração e que não receberam o diploma por motivos diversos nos anos de 2001 e 2002 é inferior a 65%.
A tabela precedente apresenta a distribuição percentual de presos no Brasil por faixa etária em 2010, segundo levantamento feito por Monteiro et al. (2011), indicando que a população prisional brasileira nesse ano era predominantemente jovem. Com base nos dados dessa tabela, julgue os itens a seguir
O desvio padrão das idades dos presos no Brasil, em 2010, foi inferior a 21 anos.
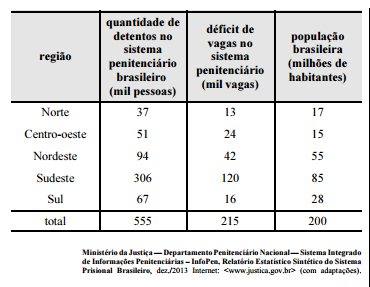
A tabela mostrada apresenta a quantidade de detentos no sistema penitenciário brasileiro por região em 2013. Nesse ano, o déficit relativo de vagas — que se define pela razão entre o déficit de vagas no sistema penitenciário e a quantidade de detentos no sistema penitenciário — registrado em todo o Brasil foi superior a 38,7%, e, na média nacional, havia 277,5 detentos por 100 mil habitantes.
Com base nessas informações e na tabela apresentada, julgue os itens a seguir.
Na análise exploratória, o histograma é um gráfico adequado para descrever a distribuição da quantidade de detentos por região em 2013.
Considerando que, entre a população carcerária de um presídio, a probabilidade de um detento contrair tuberculose seja igual a 0,01; que dois detentos sejam selecionados aleatoriamente dessa população carcerária; e que as ocorrências de tuberculose entre esses detentos sejam eventos independentes, julgue os próximos itens.
A probabilidade de os dois detentos na amostra contraírem tuberculose será igual a 0,02.
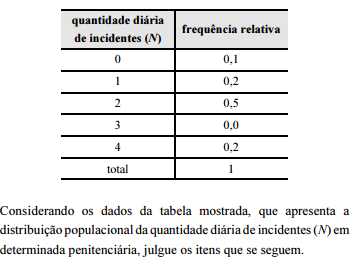
O segundo quartil da distribuição das quantidades diárias de incidentes registradas nessa penitenciária é igual a 2.
A distribuição T (t Student) é similar à distribuição Z, já que ambas são simétricas em torno da média 0 (zero). A partir dessa informação assinale a afirmativa INCORRETA.
Na estimação dos parâmetros de uma reta de regressão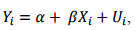 
designa-se por a e b os estimadores de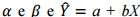 
a reta estimada. Como os estimadores a e b são funções lineares da
variável aleatória normal Y, os mesmos também são variáveis aleatórias com distribuição normal. As respectivas médias e variâncias dos estimadores a e b são:
Em uma determinada região, a população de motoristas do sexo feminino representa 48% da população total. Sabe-se que a idade média da população de motoristas do sexo feminino é 25 anos e a idade média de motoristas do sexo masculino é 40 anos. A idade média da população de motoristas é:
Em uma fábrica de apitos coloridos, a cor verde é responsável pela metade da produção, o restante é produzido nas cores amarelo e azul (40% e 10%, respectivamente). Em uma amostra com 6 apitos retirados ao acaso, foram encontrados 2 apitos de cada cor. Qual a probabilidade disso acontecer?
Uma firma de ônibus coletivos da cidade W coletou informações sobre as idades ( X) e as alturas (Y ) de 12
crianças, filhos dos motoristas, a fim de estudar se estas estavam bem nutridas. A média e o desvio padrão
das 12 idades e alturas são, respectivamente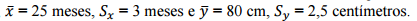 
Observou-se que a correlação entre as idades e as alturas foi r= 0,90. Um modelo de regressão linear
simples da forma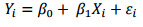 
foi ajustado. A estimativa de mínimos quadrados para 
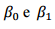é,
respectivamente:
