Suponha que o número de acidentes, envolvendo motociclistas, que ocorre diariamente em uma avenida marginal de uma
grande cidade, seja uma variável aleatória X com distribuição de Poisson com média de λ acidentes. Sabe-se que a
probabilidade de ocorrerem, diariamente, 3 acidentes é igual a probabilidade de ocorrerem 4 acidentes. Nessas condições, a
probabilidade de, em um determinado dia, ocorrer pelo menos 2 acidentes é, em %, igual a
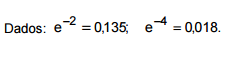
A variável aleatória X tem função densidade de probabilidade dada por:
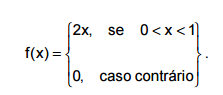
Considere a variável aleatória Y = 4X − 1. Seja g(y) a função densidade de probabilidade de Y. Nessas condições, g(y), para os
valores de Y onde essa função é diferente de zero, é dada por
Atenção: Para responder às questões de números 52 a 56 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z < 0,4) = 0,655; P(Z < 0,53) = 0,70; P(Z < 1) = 0,841; P(Z < 1,28) = 0,90; P(Z < 1,55) = 0,94; P(Z < 1,6) = 0,945; P(Z < 1,64) = 0,95; P(Z < 1,75) = 0,96; P(Z < 1,8) = 0,964; P(Z < 2,05) = 0,98
Instruções: O enunciado a seguir refere-se às questões de números 52 e 53. A porcentagem do orçamento gasto com pessoal em 40 municípios de certa região é uma variável aleatória X com distribuição normal com média μ(%) e desvio padrão 3%.
Sabe-se que a probabilidade de que o gasto com pessoal seja superior a 80% é igual a 0,02. Nessas condições, o valor de μ é,
em %, igual a
X e Y são variáveis aleatórias que representam o tempo, em minutos, de resposta à consulta aos bancos de dados A e B,
respectivamente. Sabe-se que:
I. X tem distribuição exponencial com média de 0,5 minutos;
II. Y tem distribuição exponencial com variância igual a 4(minutos)²;
III. X e Y são independentes.
Nessas condições, a probabilidade conjunta da consulta ao banco A levar menos do que 1 minuto e da consulta ao banco B
levar mais do que 2 minutos, é, em %, igual a
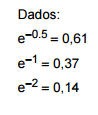
Suponha que X é uma variável aleatória discreta tal que P(X=k) = c/n para K = 1, 2, 3, 4, ...., n2, onde c é uma constante. Então, c é igual a:
Se o número médio de funcionários por vara, em uma Justiça Especializada, é de 12, enquanto a moda é de 9, é possível que a mediana do número de funcionários seja igual a:
Suponha que o número de advogados atendidos por um diretor de vara, por dia, é uma variável aleatória distribuída uniformemente entre 11 e 25, inclusive. Então, se em um dia qualquer, até certo horário, 18 advogados foram atendidos, a probabilidade de que mais de 23 sejam atendidos naquele dia é:
Considere a distribuição conjunta abaixo:
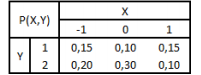
Então, P(X > -1/Y < 2) e E(X/Y =2) são respectivamente iguais a:
O Teorema do Limite Central é um dos resultados mais importantes da teoria das probabilidades. Na verdade, decorre diretamente de uma aplicação “prática” da:
Considere o experimento que consiste no lançamento de uma moeda quatro vezes. Para testar se a moeda é honesta, é feito um teste de hipóteses Ho: contra Ha: onde p é a proporção de caras. O critério de decisão estipula que se o número de caras for diferente de dois a hipótese nula deve ser rejeitada. Se, de fato, p = 0,25 a probabilidade de que o Erro do Tipo II seja cometido é:
Para explicar o estoque total de processos acumulados nas varas
de justiça (Y ) a cada ano, foi proposto um modelo de regressão
linear simples baseado no número de servidores disponíveis,
representado por X. Depois de extraída uma amostra com n = 100
foram obtidos os seguintes resultados
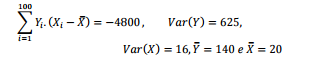
Supondo válido o modelo e significativos seus parâmetros, com
os dados acima é correto afirmar que:
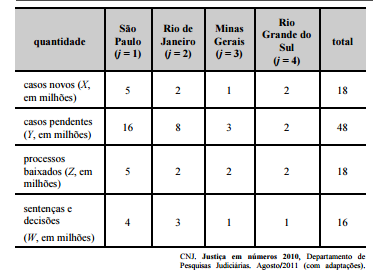
O quadro acima mostra uma síntese da movimentação processual
dos tribunais de justiça dos estados de São Paulo, Rio de Janeiro,
Minas Gerais, Rio Grande do Sul e do total da justiça estadual no
Brasil em 2010. Considere que o estoque de processos em
andamento no estado j (Ej), no final de 2010, seja um indicador que
se define como Ej= Xj+ Yj – Zj – Wj , em que j = 1, 2, ..., 27; Xj
representa o número de casos novos registrados em 2010 no
estado j; Yj seja a quantidade de casos pendentes no estado j (i.e.,
casos anteriores que não foram solucionados até o final de 2010);Zj denota o total de processos baixados (arquivados) no estado j
durante 2010 e Wj seja o número de sentenças e decisões proferidas
no estado j até o final de 2010. Considere, por fim, que, para todos
os efeitos, o Distrito Federal seja um estado. Com base nessas
informações e no quadro acima, julgue os itens que se seguem.
Considerando–se apenas os dados relativos aos estados de São
Paulo, Rio de Janeiro, Minas Gerais e Rio Grande do Sul
quanto à dispersão entre duas variáveis, é correto afirmar que
a covariância entre Z e W é superior a 1 e inferior a 2.
Nas estatísticas do Poder Judiciário, a taxa de
congestionamento (X), que consiste em um indicador que permite
medir a efetividade da movimentação processual de um tribunal, é
uma variável aleatória contínua com função de densidade
f(x) expressa por
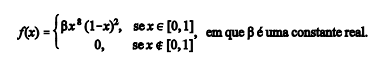
Com base nessas informações, julgue os próximos itens.
O valor de β é superior a 450 e inferior a 500.
O núcleo de assistência jurídica de um fórum que presta
assistência jurídica gratuita a pessoas carentes recebe diariamente
X casos novos, conforme uma distribuição condicional na forma
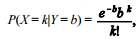em que k = 0, 1, 2, ..., b > 0 e Y segue uma
distribuição exponencial com função de densidade f(y) = 2e–2y , em que y > 0.
Considerando essa situação hipotética, julgue os itens subsequentes
Considerando essa situação hipotética, julgue os itens subsequentes.
O coeficiente de correlação linear entre as variáveis X e Y é
negativo.
O núcleo de assistência jurídica de um fórum que presta
assistência jurídica gratuita a pessoas carentes recebe diariamente
X casos novos, conforme uma distribuição condicional na forma
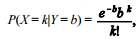em que k = 0, 1, 2, ..., b > 0 e Y segue uma
distribuição exponencial com função de densidade f(y) = 2e–2y , em que y > 0.
Considerando essa situação hipotética, julgue os itens subsequentes
Considerando essa situação hipotética, julgue os itens subsequentes.
Se o valor b for desconhecido, a quantidade média diária de
casos novos – E(X) – também será desconhecida.
