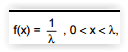Para que uma amostra seja organizada por estratos ou por conglomerados, é necessário que as unidades, para fins de sorteios, sejam organizadas por grupos, respectivamente:
Num grupo de 10 funcionários de uma empresa foi feito
um levantamento de suas alturas, que aparecem na
tabela:
Sabe-se que a média aritmética das alturas de todos
eles é 1,80 m e que a altura y tem 0,10 m a mais que a
altura x. Assim, a altura x mencionada na tabela é
A distribuição dos valores dos salários, em dezembro de 2014, dos 200 funcionários em um órgão público é representada por uma tabela de frequências absolutas, com todos os intervalos de classe apresentando a mesma amplitude, sendo fechados à esquerda e abertos à direita. O valor da mediana, obtido pelo método da interpolação linear, foi igual a R$ 5.600,00 e pertencente ao intervalo de classe, em reais, [ 5.000,00 ; 6.500,00 ). Se 80 funcionários possuem um salário inferior a R$ 5.000,00, então a porcentagem dos funcionários que apresentam um salário igual ou superior a R$ 6.500,00 é, em %, igual a
De uma população com função densidade
deseja-se obter pelo método da máxima verossimilhança, com
base em uma amostra aleatória de tamanho 6, a estimativa pontual do parâmetro λ. Os valores dos elementos da amostra, em ordem crescente, foram iguais a 4, 5, 6, 6, 7 e 8 . O desvio padrão desta população, calculado conforme a estimativa de λ, foi de
Um pesquisador, desejando comprovar se dois grupos diferem em tendências centrais, decide utilizar o teste da mediana
formulando as hipóteses:
H0 : os dois grupos provêm de populações com a mesma mediana (hipótese nula).
H1 : a mediana de um grupo difere da mediana do outro grupo (hipótese alternativa).
Neste caso, o pesquisador
O objetivo de um estudo consiste em testar a hipótese de igualdade das médias de um atributo de 3 grupos X, Y e Z, independentes, cada um contendo uma amostra aleatória de tamanho 9 . Pelo quadro de análise de variância, o valor da estatística F (F calculado) utilizado para a verificação da igualdade das médias é igual a 19 . Se a fonte de variação entre grupos apresenta um valor igual a 95, então a fonte de variação total é igual a
Considere as seguintes afirmações abaixo relativas a Séries Temporais.
I. Para o modelo Zt= 1 + at - 0,73at - 1, onde at é o ruído branco de média zero e variância 2, a previsão de origem t e
horizonte 1 é 1 - 0,73at.
II. Se a uma série temporal for ajustado um modelo ARIMA(1,0,0) com parâmetro Φ = 0,5 , a previsão dessa série de origem
t e horizonte 2 é igual ao produto do valor da série no instante t por 0,25
III. Se f(k) é função de autocorrelação de um MA(1) que tem parâmetro θ = -0,4, então 0 < f(1) < 0,35
IV. Uma técnica de diagnóstico para verificar se um modelo de série temporal representa adequadamente aos dados é o
teste do periodograma alisado.
Está correto o que se afirma APENAS em
Uma pessoa coloca um anúncio em um site de vendas com o objetivo de vender seu automóvel. Suponha que o número de
consultas que essa pessoa recebe por semana (7 dias) como resposta ao anúncio seja uma variável aleatória com distribuição
de Poisson com média igual a 3,5. Nessas condições, a probabilidade dessa pessoa receber, pelo menos, 2 consultas em um
determinado dia é, em %, igual a
Dados:
e- 0,5 = 0,61;
e- 3,5 = 0,03
Suponha que os funcionários de um determinado órgão público realizem uma tarefa em duas etapas. Sejam X1 e X2,
respectivamente, os tempos para a realização das etapas 1 e 2. Sabe-se que:
I. X1 e X2 são variáveis aleatórias independentes.
II. X1 tem distribuição normal com média igual a 2 horas e desvio padrão de 10 minutos.
III. X2 tem distribuição normal com média igual a 3 horas e variância de 300 (minutos)2
Nessas condições, a probabilidade de que um funcionário selecionado ao acaso leve, no mínimo, 270 minutos e, no máximo,
320 minutos, para a realização da tarefa é, em %, igual a
Considere:
Está correto o que se afirma APENAS em
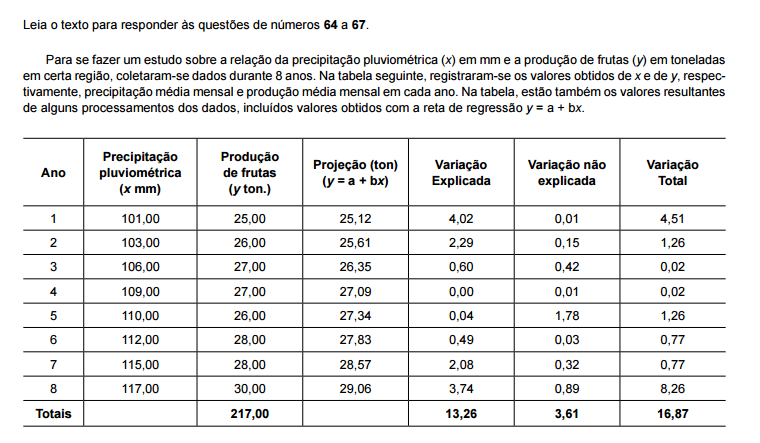
Define–se como coeficiente de determinação r2 a relação
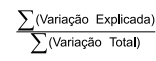
e, a partir desse valor, é possível
calcular o coeficiente de correlação, valor que mede a
“força" da relação entre as variáveis estudadas. Considerando
os dados da tabela, assinale a alternativa cujo valor
é o que mais se aproxima do coeficiente de correlação para
o caso.
Assinale a alternativa em que o histograma é o que
melhor representa a distribuição de frequência da tabela.
É correto afirmar que o percentual de jovens entre 18 e
25 anos dessa comunidade que não estudam e não trabalham
é de
A probabilidade de que saiam dois números pares e um
número impar é
Uma pesquisa revela que, em um centro de televendas,
as chamadas telefônicas ocorrem, de modo aleatório e
independente, à taxa de 12 chamadas a cada 20 minutos.
Considera–se que a probabilidade de uma chamada
é igual em quaisquer dois períodos de tempo de igual
duração e, portanto, utiliza–se a função de probabilidade
de Poisson que, para o caso, é
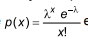em que x é
o número de chamadas em qualquer período de 20 minutos,
e λ é a média de ocorrências. De acordo com esses
dados e aproximando e–3 para 0,05, a probabilidade de
que, em 5 minutos, seja recebida exatamente uma chamada
é, aproximadamente, de
