A quantidade média de pedidos que dá entrada no almoxarifado de uma empresa medida ao longo de um ano é apresentada no seguinte histograma de frequência relativa. A mediana é aproximadamente:
Considere uma curva de frequência de uma distribuição estatística unimodal e as seguintes afirmações:
I.Os dados estão fortemente concentrados em torno da moda apresentando uma curva afilada.
II.A moda é menor que a mediana e a mediana é menor que a média.
Se a distribuição satisfaz I e II, então trata-se de uma distribuição
Uma pesquisa é realizada em uma grande cidade com uma amostra aleatória de 300 habitantes em que 75% deles manifestaram-
se favoráveis à implantação de um projeto para melhorar o atendimento ao público de sua cidade. Com base nesta
amostra, deseja-se obter um intervalo de confiança de 95% para esta proporção, considerando que a distribuição amostral da
frequência relativa dos habitantes favoráveis ao projeto é normal. Utilizando a informação da distribuição normal padrão ( Z ) que
as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,050, este intervalo de confiança é, em %, igual a
Com relação a testes de hipóteses estatísticas e denominando H0 como sendo a hipótese nula e H1 a hipótese alternativa, a
definição de potência de um teste corresponde à probabilidade de
Seja o modelo linear Yi = βXi + εi estabelecendo uma relação linear, sem intercepto, entre duas variáveis X e Y, em que Yi é a
variável dependente na observação i, Xi é a variável explicativa na observação i e εi o erro aleatório com as respectivas
hipóteses para a regressão linear simples. O parâmetro β do modelo é desconhecido e sua estimativa foi obtida pelo método dos
mínimos quadrados com base em 10 pares de observações (Xi , Yi).
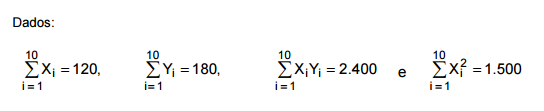
Considerando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que Y é igual a 24 quando X for igual a
Para o modelo ARMA (2,0) dado por

Está correto o que se afirma APENAS em
Atenção: Para responder às questões de números 52 a 56 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z < 0,4) = 0,655; P(Z < 0,53) = 0,70; P(Z < 1) = 0,841; P(Z < 1,28) = 0,90; P(Z < 1,55) = 0,94; P(Z < 1,6) = 0,945; P(Z < 1,64) = 0,95; P(Z < 1,75) = 0,96; P(Z < 1,8) = 0,964; P(Z < 2,05) = 0,98
Tendo por base

Os valores simulados de uma distribuição normal com média 10 e desvio padrão 2, a partir de u1, u2, u3, são dados, respectivamente,
por
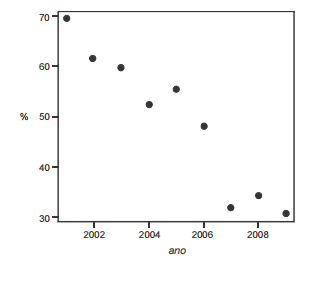
Dado que a participação dos presidiários em cursos de qualificação profissional é um aspecto importante para a reintegração do egresso do sistema prisional à sociedade, foram realizados levantamentos estatísticos, nos anos de 2001 a 2009, a respeito do valor da educação e do trabalho em ambientes prisionais. Cada um desses levantamentos, cujos resultados são apresentados no gráfico, produziu uma estimativa anual do percentual P de indivíduos que participaram de um curso de qualificação profissional de curta duração, mas que não receberam o diploma por motivos diversos. Em 2001, 69,4% dos presidiários que participaram de um curso de qualificação profissional não receberam o diploma. No ano seguinte, 2002, esse percentual foi reduzido para 61,5%, caindo, em 2009, para 30,9%. A partir das informações e do gráfico apresentados, julgue os itens que se seguem.
Os dados apresentados são suficientes para que se possa afirmar que o total de presidiários que participaram de um curso de qualificação profissional de curta duração e que não receberam o diploma em 2008 foi superior ao total referente ao ano de 2007.
A tabela precedente apresenta a distribuição percentual de presos no Brasil por faixa etária em 2010, segundo levantamento feito por Monteiro et al. (2011), indicando que a população prisional brasileira nesse ano era predominantemente jovem. Com base nos dados dessa tabela, julgue os itens a seguir
A curtose é uma medida de variação que representa a semiamplitude de uma distribuição de dados e, por isso, seu valor na distribuição percentual de presos no Brasil em 2010 foi igual a 21 anos.
A tabela precedente apresenta a distribuição percentual de presos no Brasil por faixa etária em 2010, segundo levantamento feito por Monteiro et al. (2011), indicando que a população prisional brasileira nesse ano era predominantemente jovem. Com base nos dados dessa tabela, julgue o item a seguir
A maior parte da população prisional brasileira em 2010 era formada por pessoas com idades inferiores a 30 anos. Porém, a média da distribuição das idades dos presos no Brasil nesse ano foi superior a 30 anos.
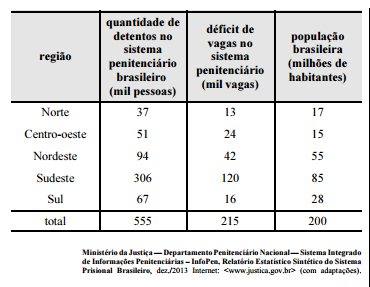
A tabela mostrada apresenta a quantidade de detentos no sistema penitenciário brasileiro por região em 2013. Nesse ano, o déficit relativo de vagas — que se define pela razão entre o déficit de vagas no sistema penitenciário e a quantidade de detentos no sistema penitenciário — registrado em todo o Brasil foi superior a 38,7%, e, na média nacional, havia 277,5 detentos por 100 mil habitantes.
Com base nessas informações e na tabela apresentada, julgue os itens a seguir.
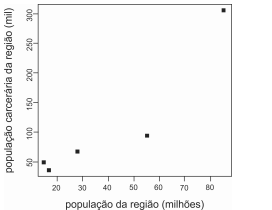
Considerando que a figura a seguir apresente o diagrama
de dispersão entre o tamanho populacional da região
(em milhões de habitantes) e a população carcerária
correspondente (em mil pessoas), então é correto afirmar
que a população carcerária tende a crescer linearmente à
medida que a população da região aumenta
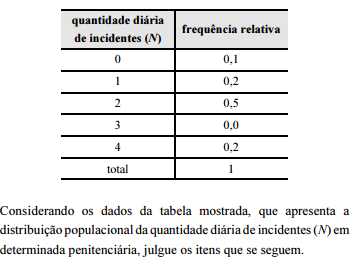
A amplitude total da distribuição é igual a 5, pois há cinco valores possíveis para a variável N.
Ao instrumento usado para fazer a adequação entre o raciocínio e a realidade deu-se o nome de modelo. A partir dessa informação, marque V para as afirmativas verdadeiras e F para as falsas. ( ) Um modelo pode ser definido como uma síntese dos dados. ( ) Qualquer distribuição estatística pode se enquadrar em dois tipos de modelos: determinístico ou estocástico. ( ) Um modelo não pode ser definido como uma hipótese ou como uma ideia estruturada. ( ) Um modelo pode ser construído utilizando como instrumento de cálculo a probabilidade. Assinale a sequência correta.
Um teste de significância avalia a evidência proporcionada pelos dados em favor de alguma informação da população. Sobre esse assunto, assinale a afirmativa correta.
Suponha que a vida útil de dois radares seja independente uma da outra e que o primeiro radar tenha vida média esperada de 1000 horas, enquanto o segundo radar tenha vida média esperada de 1200 horas. A probabilidade de que ambas as vidas úteis sejam de no mínimo 1500 horas é: