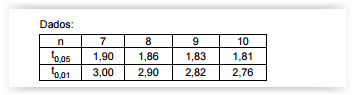
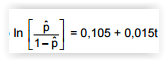Atenção: Para responder às questões de números 41 a 43, considere as informações abaixo.
A tabela a seguir apresenta a distribuição de frequências conjunta das variáveis sexo e salário, relativas a um grupo de 200 funcionários de um órgão público. A variável salário está representada por faixas de salário em número de Salários Mínimos − SM.
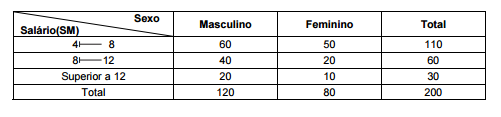
Um funcionário será selecionado ao acaso desse grupo, a probabilidade dele não ter salário na faixa 8 12 ou ser do sexo feminino, é, em %, igual a
A função densidade de probabilidade do tempo, em horas, requerido para completar uma tarefa realizada por funcionários de um determinado departamento de um órgão público tem distribuição uniforme contínua no intervalo [a - b; a + b], onde a e b são números reais positivos, cuja unidade é hora e a > b. Sabe-se que o tempo médio para a conclusão da tarefa é igual a 11 (horas) e a variância do tempo para conclusão da tarefa é de 3 (horas)2. Nessas condições, a probabilidade do tempo requerido para a conclusão da tarefa ser inferior a c = 4b (horas) é igual a
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
Sejam X1, X2... Xn variáveis aleatórias independentes e identicamente distribuídas com distribuição normal padrão. Sejam as variáveis aleatórias:
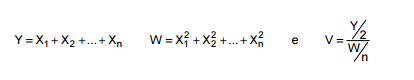
Considere:
I. A função geratriz de momentos de Y, quando n = 2, é m(t) = e 2t .
II. A variável W tem distribuição qui-quadrado com (n − 1) graus de liberdade.
III. A variável V tem distribuição F de Snedecor com graus de liberdade 2 e n.
IV. Para n = 4, P(− 2 < Y < 1) = 0,432.
Está correto o que consta APENAS em
Para o atendimento de reclamações trabalhistas um determinado órgão público disponibilizou um único guichê de atendimento.
Suponha que os requerentes cheguem ao guichê à taxa de 1/6 minutos (um a cada 6 minutos). O funcionário que atende os
requerentes completa o atendimento à taxa de 1/5 minutos (um a cada 5 minutos). Considere para esse modelo de fila o M/M/1.
Nessas condições, o tempo médio que cada requerente permanece na fila, em minutos, é igual a
Considerando duas variáveis aleatórias independentes X e Y que
seguem distribuições normal padrão, julgue o próximo item.
A diferença X-Y segue uma distribuição normal cuja variância
é igual ou inferior a 1
Em uma população a probabilidade de que um indivíduo tenha cometido crimes contra o patrimônio é de 0,024 e contra pessoas é de 0,043. Já a probabilidade de que tenha cometido ambos os crimes é de 0,018. Então, a probabilidade de que o indivíduo tenha cometido ao menos um dos crimes é de:
Sabe-se que o tempo de duração de um processo na justiça do trabalho é uma variável aleatória contínua distribuída exponencialmente, com média de 1200 dias. Se já passaram 900 dias de um processo, a probabilidade de que ele dure mais do que 1500 dias é igual a:
Seja X uma variável aleatória contínua com função distribuição acumulada fx (x ). Outra variável, Y, é definida por Y = fx (x ).Então a distribuição acumulada de Y é dada por:
Se X1= 2, X2= -1, X3=3 e X4=4 é o resultado da extração de uma amostra aleatória simples (n=4), a estimativa do 3º momento ordinário da população, através do método dos momentos, é igual a:
Num modelo de regressão linear, a violação dos pressupostos de homocedasticidade e do emprego de variáveis explicativas não estocásticas, mantidas as demais hipóteses, poderá causar a perda, por parte dos estimadores de MQO, respectivamente, das propriedades de:
Para fins da análise dos resíduos de uma regressão múltipla,
apurou-se a seguinte tabela de decomposição amostral.

Em uma escola é realizado um censo apurando-se as alturas de todos os 180 estudantes em centímetros (cm). A média
aritmética das alturas dos 100 estudantes do sexo masculino foi igual a dos 80 estudantes do sexo feminino. Se Xi representa a
altura do i-ésimo estudante do sexo masculino e Yj a altura do j-ésimo estudante do sexo feminino, obteve-se
Se o desvio padrão das alturas dos estudantes do sexo masculino foi igual a 10 cm, o coeficiente de variação considerando
todos os estudantes desta escola é, em %, de
Sejam E1 = 4mX - 6nY - Z e E2 = mX + nY - 7Z dois estimadores não viesados para a média μ de uma população normal com variância unitária. Considere que (X, Y, Z) é uma amostra aleatória desta população, com reposição, sendo m e n parâmetros reais. O estimador mais eficiente, entre E1 e E2, apresenta uma variância igual a
O desvio padrão de uma população normal de tamanho infinito é desconhecido e deseja-se saber se a média μ desta população
é inferior a 17,5 a um nível de significância α. Foram formuladas as hipóteses H0: μ = 17,5 (hipótese nula) e H1: μ < 17,5
(hipótese alternativa). Uma amostra aleatória de tamanho 9 é extraída desta população, observando-se que a média amostral foi
igual a 15 e a soma dos quadrados de todos os elementos da amostra foi igual a 2.097. Considerando que tα o quantil da
distribuição t de Student para o teste unicaudal tal que a probabilidade P(t > tα) = α, com n graus de liberdade, tem-se com base
na amostra que H0
O gerente de uma loja utiliza a equação de regressão
para estimar a probabilidade (p) de ocorrer a
venda de um determinado equipamento em função do tempo (t) diário, em minutos, em que o equipamento fica exposto na vitrine da loja. Dado que o equipamento fica exposto na vitrine durante 20 minutos, em um dia, a probabilidade de ocorrên- cia de venda do equipamento é, em %, de
Dado:
ln (1,5) = 0,405
Observação:
ln é o logarítmo neperiano, tal que ln (e) = 1, e os parâmetros da
equação foram obtidos pelo método dos mínimos quadrados.