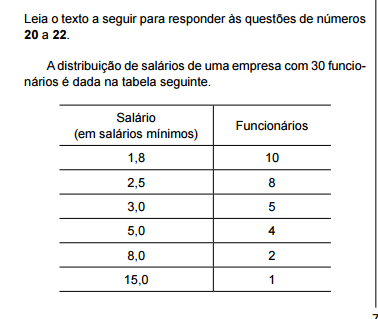
A tabela 2X2 abaixo fornece o número de motoristas do sexo masculino e o de motoristas do sexo feminino
que responderam a um teste de renovação da CNH.
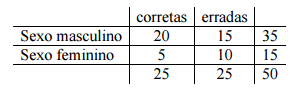
Os valores da tabela de frequências esperadas para o número de motoristas do sexo masculino que poderiam
ter dado resposta correta e o número de motoristas do sexo feminino que poderiam ter dado resposta errada
são, respectivamente:
INSTRUÇÃO: Analise o texto abaixo e responda às questões 93 e 94.
O Box-plot (diagrama de caixas) é um gráfico utilizado para verificar a distribuição de uma variável quantitativa. Segundo o Detran, os três tipos de veículos mais frequentes em circulação no município de Cuiabá são: Automóvel, Motocicleta e Caminhonete. Foi feito um levantamento sobre as velocidades em que cada um desses três tipos de veículos foi multado ao passar por um radar onde a velocidade máxima permitida era 60 km/h.
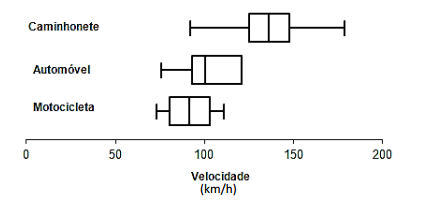
A partir das informações dadas, assinale a afirmativa correta.
O Detran verificou que um tipo de pneu, utilizado em seus veículos, percorria até estourar, em média 30000 km, com desvio padrão de 300 km, segundo uma distribuição normal. Qual a probabilidade do pneu estourar antes de 30000 km?
Durante um período de 40 dias úteis, realizou-se um levantamento com relação a quantidade de reclamações trabalhistas em
uma região. O quadro abaixo apresenta a quantidade de reclamações correspondente a este levantamento.
Sabendo-se que a mediana da distribuição é igual a 2,5, obtém-se que o resultado do produto da moda pela média aritmética
(reclamações por dia) é
Uma amostra aleatória (X , Y) é extraída, com reposição, de uma população normalmente distribuída com média μ e variância σ² diferente de zero. Deseja-se obter uma estimativa de μ com a utilização da classe de estimadores não viesados E = 2mX + nY, sendo m e n parâmetros reais. Dentre todos os estimadores determinados por esta classe é escolhido aquele que é o mais eficiente. Isto significa que o valor de m é igual a
Em duas grandes empresas E1 e E2 são selecionados aleatoriamente 50 empregados de E1 e 150 empregados de E2. Foi
perguntado a cada um dos empregados se eles eram a favor da substituição dos equipamentos da sua empresa. Supondo que
esta pesquisa tenha sido realizada independentemente, o resultado pode ser visualizado pela tabela abaixo.
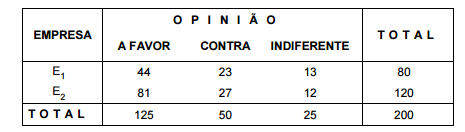
Com base nos dados desta tabela, deseja-se testar, ao nível de significância de 10%, se a opinião dos empregados depende da
empresa em que trabalham. Utilizou-se então o teste qui-quadrado para esta tomada de decisão.
Conclui-se que, ao nível de significância de 10%, a opinião dos empregados
Para um determinado ramo de atividade, o modelo linear correspondente à equação Yi = α + βXi + γSi + ∈i (i = 1, 2, 3, ...) foi
construído para estimar o salário mensal (Yi), em reais, em função do número de anos de experiência (Xi) e do sexo (Si ) do
trabalhador (i refere-se ao i-ésimo trabalhador). Considera-se no modelo que Si = 1 se o trabalhador for homem e Si = 0 se o trabalhador for mulher. Os parâmetros α, β e γ são desconhecidos e ∈i é o erro aleatório com as respectivas hipóteses da
correspondente regressão. As estimativas de α, β e γ (a, b e c, respectivamente) foram obtidas pelo método dos mínimos
quadrados com base em n observações e todas foram estritamente positivas. Considerando todos os trabalhadores deste ramo
de atividade e utilizando a função obtida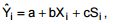 
Atenção: Para responder às questões de números 41 a 43, considere as informações abaixo.
A tabela a seguir apresenta a distribuição de frequências conjunta das variáveis sexo e salário, relativas a um grupo de 200 funcionários de um órgão público. A variável salário está representada por faixas de salário em número de Salários Mínimos − SM.
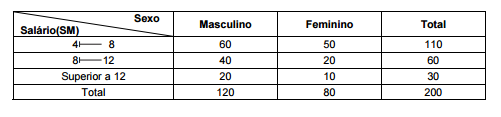
Quatro funcionários serão selecionados ao acaso e com reposição desse grupo. A probabilidade de que pelo menos dois sejam
do sexo masculino e ganhem pelo menos 8 SM é igual a
Considere a variável aleatória contínua X com função densidade de probabilidade dada por:
Se Mo( X) representa a moda de X, então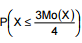 
é igual a
Sabe-se que a função de distribuição conjunta das variáveis X e Y é dada por
Nessas condições, P(0,3 < X < 0,7) é, em %, igual a
Sejam Y1, Y2, Y3 as estatísticas de ordem de uma amostra aleatória de tamanho 3 de uma distribuição com função densidade
dada por f(x ) = e − x, para x > 0 e zero no complementar. Nessas condições, P(Y1 < 0,5) é igual a
Resultados de uma pesquisa declaram que o desvio
padrão da média amostral é 32. Sabendo que o desvio
padrão populacional é 192, então o tamanho da amostra
que foi utilizada no estudo foi
Uma empresa alimentícia produz um artigo em pacotes
de 200 gramas em média, com desvio padrão de
2 gramas e distribuição normal. É realizado um teste de
controle de qualidade em que, periodicamente, sorteia–
–se uma amostra aleatória de 4 pacotes e, se a média
da amostra for superior a 202 gramas ou inferior a 198
gramas, a produção é interrompida para manutenção das
máquinas. Se a média se alterou para 201 gramas, e o
desvio padrão se mantém em 2 gramas, a probabilidade
de parar a produção é de, aproximadamente,
