Sejam X e Y dois eventos:
X: um motorista possui cartão A para pagamento de taxas do Detran;
Y: um motorista possui cartão B para pagamento de taxas do Detran.
Supondo-se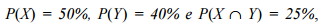 
a probabilidade de um motorista selecionado aleatoriamente ter pelo menos um dos dois tipos de cartão é:
Determinado estudo com 2000 motoristas foi conduzido para verificar se há ou não associação entre as variáveis “hábito de fumar” (1000 fumantes e 1000 não fumantes) e “presença de câncer” (1100 motoristas com câncer e 900 sem câncer). Sabendo que há 650 motoristas não fumantes e sem câncer, construa uma tabela de contingência 2?2, e marque V para as afirmativas verdadeiras e F para as falsas. ( ) A tabela de contingência contém 4 graus de liberdade. ( ) Há 35% de motoristas com câncer entre os não fumantes. ( ) Há 25% de motoristas fumantes entre aqueles sem câncer. ( ) Há 750 motoristas fumantes e com câncer. Assinale a sequência correta.
INSTRUÇÃO: Analise o texto abaixo e responda às questões 93 e 94.
O Box-plot (diagrama de caixas) é um gráfico utilizado para verificar a distribuição de uma variável quantitativa. Segundo o Detran, os três tipos de veículos mais frequentes em circulação no município de Cuiabá são: Automóvel, Motocicleta e Caminhonete. Foi feito um levantamento sobre as velocidades em que cada um desses três tipos de veículos foi multado ao passar por um radar onde a velocidade máxima permitida era 60 km/h.
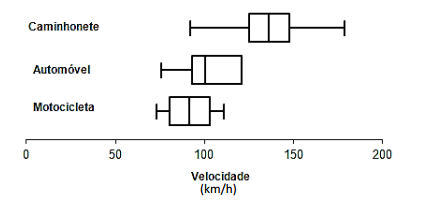
A partir da figura, assinale a afirmativa correta.
Um estatístico, ao fazer um gráfico de uma variável quantitativa, observa que a distribuição é assimétrica à esquerda. Dessa observação, ele pode concluir:
Em um censo realizado em um clube apurou-se a altura em centímetros (cm) de seus 200 associados. A média aritmética
apresentou um valor igual a 160 cm com um coeficiente de variação igual a 18,75%. O resultado da divisão da soma de todos os
valores das alturas elevados ao quadrado pelo número de associados é, em cm2, de
Uma amostra aleatória de tamanho 256 é extraída de uma população normalmente distribuída e considerada de tamanho
infinito. Considerando que o desvio padrão populacional é igual a 100, determinou-se, com base na amostra, um intervalo de
confiança de 86% igual a [890,75 ; 909,25]. Posteriormente, uma nova amostra de tamanho 400, independente da primeira, é
extraída desta população, encontrando-se uma média amostral igual a 905,00. O novo intervalo de confiança de 86% é igual a
Durante uma semana, observa-se a quantidade de determinadas ocorrências, esperando que diariamente ocorram 20 destes
tipos de ocorrências. Para esta análise, foram levantados os seguintes dados em uma semana escolhida aleatoriamente:
qui-quadrado. Foram formuladas as hipóteses H0: as frequências são iguais em todos os dias da semana (hipótese nula) e H1:
as frequências são diferentes.
Observação: o valor crítico do qui-quadrado tabelado da distribuição qui-quadrado, ao nível de significância de α e com o respectivo número de
graus de liberdade do teste, apresentou um valor superior ao valor do qui-quadrado observado.
O valor do qui-quadrado observado é
A função densidade de probabilidade da variável aleatória contínua X é dada por:
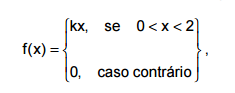
onde k é uma constante apropriada para garantir que f(x) seja uma função densidade de probabilidade. Selecionando-se,
aleatoriamente e com reposição, 5 valores de X dentro do intervalo 0 < x < 2, a probabilidade de que exatamente 3 sejam
inferiores a 1 é igual a
Atenção: Para responder às questões de números 52 a 56 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z < 0,4) = 0,655; P(Z < 0,53) = 0,70; P(Z < 1) = 0,841; P(Z < 1,28) = 0,90; P(Z < 1,55) = 0,94; P(Z < 1,6) = 0,945; P(Z < 1,64) = 0,95; P(Z < 1,75) = 0,96; P(Z < 1,8) = 0,964; P(Z < 2,05) = 0,98
Seja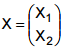 
um vetor de variáveis aleatórias com distribuição normal bivariada com vetor de médias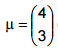 
matriz de covariâncias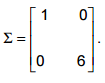 
Considere a variável aleatória bidimensional Y, formada por combinações lineares de X, dada por:
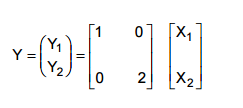
Sendo W = Y1 + Y2, a probabilidade denotada por P(2 < W < 8) é, em %, igual a
Considere as seguintes afirmações:
Está correto o que se afirma APENAS em
A distribuição normal é uma das mais importantes
distribuições de probabilidade da estatística. Também
conhecida como distribuição gaussiana, apresenta
propriedades importantes para a realização de modelagens e
inferências estatísticas sobre diversas variáveis estudadas.
Em relação à distribuição normal e a suas propriedades,
assinale a alternativa correta.
Em um histograma representando os preços unitários de microcomputadores em estoque, observa-se que no eixo das abscissas constam os intervalos de classe em R$ e no eixo das ordenadas as respectivas densidades de frequências em (R$)-1. Densidade de frequência de um intervalo de classe é o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo. Um determinado intervalo de classe com amplitude igual a R$ 2.500,00 apresenta uma densidade de frequência, em (R$)-1, igual a 12,8 × 10-5. Se o número de microcomputadores deste intervalo é igual a 48, então o número total de microcomputadores em estoque é igual a
A distribuição referente a uma variável aleatória X com média 25 é desconhecida. Utilizando o Teorema de Tchebichev foi apurado que a probabilidade mínima de X pertencer ao intervalo (22 , 28) é igual a 96%. O coeficiente de variação de X é, em %, igual a
De uma população normal e de tamanho infinito com o desvio padrão populacional igual a 4 extrai-se uma amostra aleatória de
tamanho 64. Com base nesta amostra, deseja-se saber, ao nível de significância de 5%, se a média μ desta população é inferior
a 30. Foram formuladas as hipóteses H0: μ = 30 (hipótese nula) e H2: μ < 30 (hipótese alternativa) com utilização das
informações da curva normal padrão (Z ) que as probabilidades P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10. O menor valor
encontrado para a média amostral
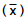
al que H0 não é rejeitada apresenta um valor igual a
Um modelo regressivo linear múltiplo correspondente à equação Zi = α + βXi + γYi + ∈i
(i = 1, 2, 3, ... ) foi construído para prever Z em função de X e Y. Os parâmetros α, β e γ são desconhecidos, ∈i
corresponde ao erro aleatório com as respectivas hipóteses
do modelo de regressão linear múltipla e i refere-se à i-ésima observação. Com base em 21 observações e utilizando o método
dos mínimos quadrados obtiveram-se as estimativas de α, β e γ (a, b e c, respectivamente).
O valor da estatística F (F calculado) que permite decidir por meio da comparação com o F tabelado sobre a existência da
regressão é igual a
