Em estudo acerca da situação do CNPJ das empresas de determinado município, as empresas que estavam com o CNPJ regular foram representadas por 1, ao passo que as com CNPJ irregular foram representadas por 0. Considerando que a amostra {0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1} foi extraída para realizar um teste de hipóteses, julgue os itens subsequentes.
Sendo P(Z > 1,96) = 0,025 e P(Z > 1,645) = 0,05,
em que Z representa a variável normal padronizada,
e P(t20 > 2,086) = 0,025 e P(t19 > 1,729) = 0,05, em que t20 e t19
possuem distribuição t de Student com, respectivamente,
20 e 19 graus de liberdade, o erro utilizado para a construção
do intervalo de confiança é menor que 15%, se considerado
um nível de significância de 5%.
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α² = 4
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
Onde,
é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α² = 4
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
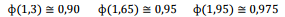
Onde,
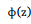é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Considerando-se que apenas os 10% que atinjam as maiores notas serão aprovados, a nota mínima para aprovação é:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E(X ) = 4, V (Y ) = 16, (X,Y) = 6 .
Então a variância de Z é:
Para estudar o peso dos peixes de um tanque, foi feito um estudo amostral e coletado uma amostra aleatória de 10 peixes. Os pesos em kg dos peixes são mostrados a seguir: 5 4 3 3 6 7 7 2 8 5 Qual o Coeficiente de Variação (CV) do peso dos peixes da amostra retirada desse tanque?
Uma empresa de chocolates deseja averiguar se o peso das barras de chocolate que produz é igual ou diferente do
indicado nas embalagens, que é de 100 gramas. Para tanto, foi feito um estudo amostral e coletado o peso de 36
barras de chocolate de maneira independente, cujo peso médio foi 104 gramas. Sabendo que a variância
populacional é de 16 gramas2, faça um intervalo com 95% de confiança para a média e calcule a estatística de teste
para a hipótese do peso ser igual ou diferente do especificado nas embalagens.
Assinale a alternativa correta.
Considere as seguintes distribuições de probabilidade:
- Distribuição Binomial;
- Distribuição de Poisson;
- Distribuição Normal; e,
- Distribuição Exponencial.
Selecione a alternativa que contém, dentre as distribuições listadas, as que pertencem à Família Exponencial.
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X, sendo E(X²) = 25, E(X ) = 4, Var(Y ) 16,Cov (X,Y) . Então a variância de Z é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
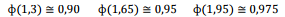
Onde,
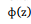é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
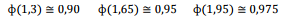
Onde,
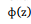é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
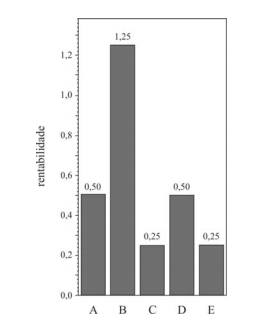
A probabilidade do fundo de investimento E é maior que a
probabilidade do fundo de investimento C.
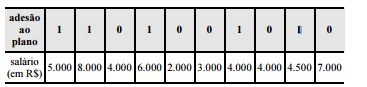
Considerando que os dados na tabela mostram salários de diferentes servidores que aderiram (1) ou não aderiram (0) a determinado plano de previdência complementar, julgue os itens subsecutivos.
O método de Newton Raphson é uma forma numérica
que pode ser utilizada para estimar os parâmetros em um
modelo de regressão logística, visto que os estimadores não
possuem forma fechada. O mesmo pode ser feito em um
modelo de regressão linear, apesar de a forma deste ser
fechada para o estimador dos parâmetros.
Em um levantamento feito para avaliar a adesão de empresas a determinados padrões contábeis, considerou-se uma variável quantitativa X, tal que X = 1, se a empresa observada no levantamento seguir os padrões; ou X = 0, se a empresa não seguir os padrões. Considerando-se que a média amostral da variável X seja igual a 0,8, e que a amostra consista de 17 empresas, é correto afirmar que a variância amostral s2 de X é tal que
