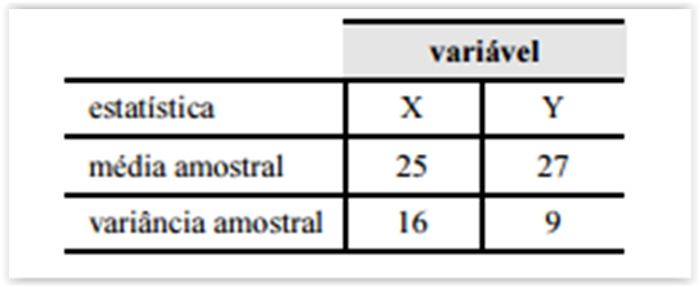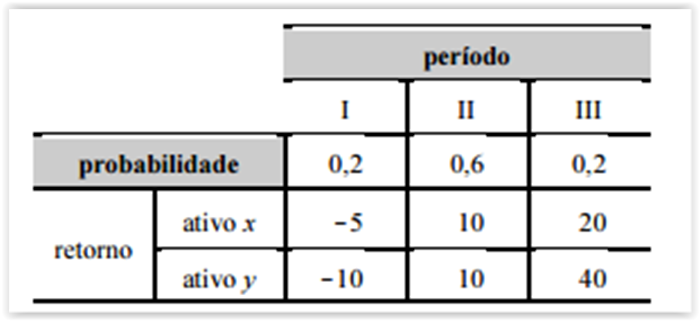
A tabela precedente mostra os ativos x e y (variáveis aleatórias) e seus retornos. Considerando que as variâncias de x e y sejam
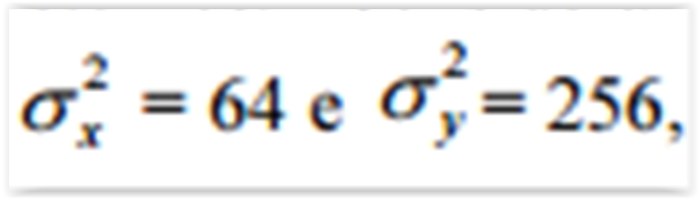
O retorno esperado do ativo x é superior ao retorno esperado
do ativo y
Se as variáveis X e Y forem independentes, o desvio padrão da
soma X + Y será igual a 7.
Considerando que Z represente uma distribuição normal padrão, julgue os próximos itens.
O valor esperado da variável aleatória Z(Z – 1) é igual a 1.
Considere uma população normal com média µ e desvio padrão conhecido s. A partir de uma amostra de tamanho 144 dessa
população, construiu-se um intervalo de confiança de 95% para µ com amplitude igual a 5. Assinale a opção que corresponde
ao valor de s. (Considere o quantil de ordem 97,5% da distribuição normal padrão como aproximadamente 2).
A figura seguinte ilustra o editorial do dia 25.01.2015 de
um grande jornal paulista, que trata de questões relacionadas
à crise de abastecimento de água que vem se
agravando nos últimos meses na região metropolitana de
São Paulo. Os valores anotados referem–se ao nível em
percentual do volume de água presente no Sistema Cantareira
em cada uma das datas, tomando–o em relação à
capacidade total do sistema.
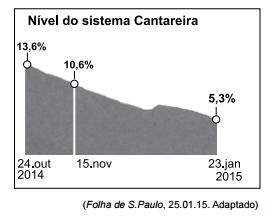
De acordo com os valores apresentados na figura, é
correto afirmar que
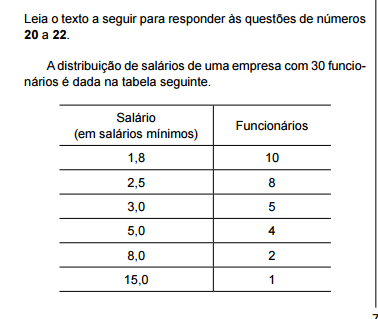
Considerando–se a média dos salários, o valor do desvio
do salário de quem ganha R$ 1.400,00 mensais é
Suponha que 10% da população seja composta de fumantes.
Ao se tomar uma amostra aleatória de 100 pessoas da
população, a probabilidade de haver mais de 15 fumantes
na amostra é de, aproximadamente,
Supondo–se que a distribuição seja normal com desvio
padrão de R$ 120,00 e que a amostra dos 16 dias tenha
acusado o valor de R$ 910,00, então o intervalo de confiança
para a verdadeira média com 95% de confiança é
de, aproximadamente,
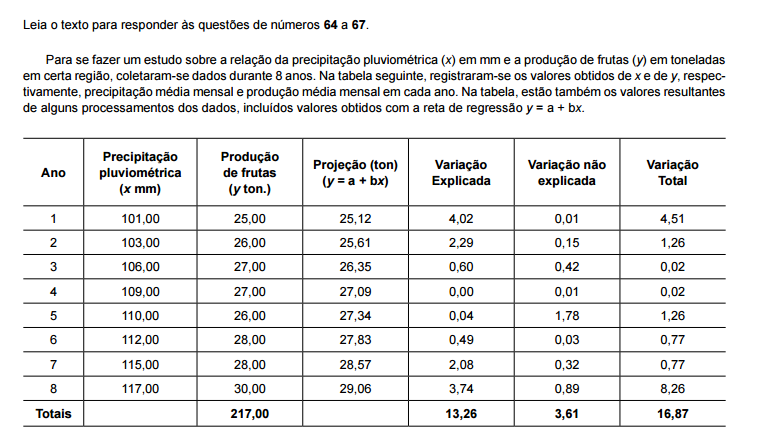
Os dados da tabela permitem ainda concluir que p por
cento das variações da produção de frutas podem ser
explicadas pela variação da precipitação pluviométrica.
O valor mais próximo de p, para esse caso, é
O número de falhas mensais de um computador é uma variável que tem distribuição de Poisson com média λ. Sabe–se que λ é
igual à média de uma distribuição uniforme no intervalo [2, 4]. Nessas condições, a probabilidade de o computador apresentar
exatamente duas falhas no período de 15 dias é igual a
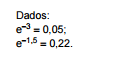
As afirmações a seguir, todas verdadeiras, foram feitas pelo chefe do departamento de Imunologia de uma faculdade de
medicina, referindo–se a eventos que poderiam acontecer no ano de 2014
1– Se o projeto for aprovado, o departamento receberá novos computadores e terá seu laboratório reformado.
2– Se o laboratório for reformado, passará a ter capacidade para processar o sangue de 50 pacientes por dia.
3– Se for possível processar o sangue de 50 pacientes por dia, o número de atendimentos diários no ambulatório será
duplicado.
A partir dessas informações, é correto concluir que, se a capacidade de processamento de sangue do laboratório do
departamento de Imunologia, em 2015, é de apenas 25 pacientes por dia, então, necessariamente,
Admite-se que o número de peças (x ) que se danificam em um pacote com 4 peças cada um, durante o transporte do depósito
até a fábrica, obedece à lei de Poisson
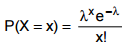
Observando, aleatoriamente, 400 destes transportes, decide-se
estimar pelo método da máxima verossimilhança o parâmetro