Sobre a regressão linear analise as afirmativas:
I. A variável independente também pode ser chamada de regressora e/ou explicativa, sendo considerada a variável principal.
II. A regressão Linear tem a finalidade de avaliar o comportamento de uma variável em função daoutra.
III. A variável dependente é aquela cujo valor é observado em função da variável principal (a variável independente).
De acordo com as afirmativas acima, quais estão corretas:
É uma técnica que busca localizar os valores dos parâmetros que ampliam a função de verossimilhança, que mede a probabilidade dos dados pesquisados dado o modelo. Esse método é amplamente utilizado e pode ser aplicado a diversostipos de modelos, como regressão linear, modeloslineares generalizados e outros. Esse conceito refere-se a
A Estatística pode ser definida como a ciência que estuda os processos de coleta, organização, análise e interpretação de dados numéricos variáveis referentes a qualquer fenômeno. A estatística divide-se em 3 grandes partes: descritiva, probabilística e inferencial. Qual das assertivas abaixo refere-se à estatística descritiva?
Considerados dois eventos aleatórios E1 e E2, tais que P( E1 ∩ E2 | E1)= 0,3, P( E1 | E2 )= 0,4 e P( E1 ∪ E2 )= 0,87, o valor da probabilidade de ocorrência do evento E1 é igual a
Suponha que uma amostra aleatória simples 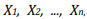 de tamanho n, será observada para se estimar a média
de tamanho n, será observada para se estimar a média 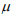 de uma variável populacional suposta normalmente distribuída com média
de uma variável populacional suposta normalmente distribuída com média 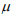 e variância
e variância 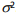 .
.
O pesquisador cogita usar a média amostral 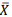 como estimador de
como estimador de 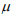 Avalie se, nessas condições, as seguintes afirmativas acerca das
Avalie se, nessas condições, as seguintes afirmativas acerca das
propriedades de 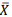 estão corretas:
estão corretas:
I.
Suponha que uma amostra aleatória simples 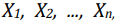 de tamanho n, será observada para se estimar a média
de tamanho n, será observada para se estimar a média 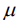 de uma
de uma
variável populacional suposta normalmente distribuída com média 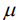 e variância
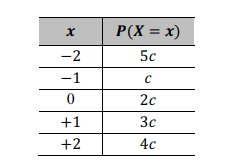
e variância 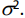
O pesquisador cogita usar a média amostral
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A mediana de X é igual ou superior a 1.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
A probabilidade de ocorrência simultânea dos eventos V < 0 e W < 0 é igual a 0,21.
Supondo que os valores 3, 0, 0, 1, 4 constituam uma realização de uma amostra aleatória simples de tamanho n igual a 5 retirada de uma população com função de probabilidade
![]() denota o parâmetro a ser estimado e x ∈ {0, 1, 2, … }, julgue o seguinte item.
denota o parâmetro a ser estimado e x ∈ {0, 1, 2, … }, julgue o seguinte item.
A estimativa de máxima verossimilhança da probabilidade P (X = 0) é igual à frequência relativa de zeros na amostra, ou seja, 2/5
Em modelos de dados em painel com efeito fixo, presume-se que as características individuais não observáveis que são constantes no tempo estão correlacionadas com as variáveis
explicativas.
Um banco oferece dois serviços aos seus clientes. Sabe-se, no entanto, que 20% dos clientes não contratam qualquer um deles, 50% contratam apenas um e os 30%
restantes contratam os dois serviços oferecidos.
Qual é a média do número de serviços contratados pelos clientes desse banco?
De uma amostra aleatória simples de tamanho n = 400 retirada de uma população normal, obteve-se as seguintes estatísticas.

Deseja-se testar a hipótese H0: μ ≥ 20 contra a hipótese H1: μ < 20 com nível de significância de 5%, na qual μ denota a média populacional. Sabendo que P(Z < 1,645) = 0,95, em que Z é uma variável aleatória normal padrão, assinale a opção correta.
A equação y = mx + b, com m = 2,09 e b = 0,257, foi obtida na calibração de um método para a determinação cromatográfica de isoctano em misturas de hidrocarbonetos. Nessa equação, o eixo x apresenta valores de concentração de isoctano, em porcentagem molar, e o eixo y, a área sob o pico cromatográfico, em uma unidade arbitrária.
Tendo como referência as informações precedentes, julgue os itens subsecutivos, a respeito de fundamentos de estatística.
No método dos mínimos quadrados, os valores calculados de xi, yi, xi2, yi2, xiyi e seus respectivos somatórios devem ser
arredondados para três algarismos significativos antes de se calcular os demais parâmetros da regressão linear.
Um órgão governamental precisa analisar a distribuição da população por faixa salarial, a partir de dados individuais doimposto de renda anonimizados. Para isso, dividirá os salários em faixas, para gerar um gráfico que indique a quantidade de contribuintes cujo salário está dentro de cada uma dessas faixas.
Para esse fim, a visualização gráfica mais adequada é o
Considere a seguinte Tabela de valores críticos da estatística x2 ao nível de significância 5%:

Uma política pública visava capacitar profissionais em situação de desemprego, para facilitar-lhes a reinserção no mercado de trabalho.
Um estudo acerca da efetividade dessa política tomou uma amostra aleatória de 100 profissionais desempregados que
foram capacitados no âmbito dessa política e outros 200 profissionais desempregados que, embora elegíveis para serem
capacitados, não o foram.
A análise descritiva da amostra concluiu que, um ano após o término do curso, 80 profissionais dentre os 100 profissionais
que foram capacitados estavam empregados e 100 profissionais dentre os 200 profissionais que não foram capacitados também estavam empregados.
Com o intuito de avaliar a efetividade dessa política pública, faz-se, dentre outras análises, um teste de independência x2
que verifica se há (ou não) relação entre ter realizado a capacitação profissional e ser reinserido no mercado de trabalho.
Ao nível de significância de 5%, conclui-se que a política pública

