Considere que N(t) representa a quantidade de veículos que chegam ao estacionamento de um tribunal durante o intervalo de tempo t (em minutos). Suponha que N(t) segue um processo de renovação, de maneira que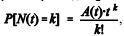
em que A(t) > 0 é uma constante de normalização. Nesse caso, é correto afirmar que o intervalo de tempo entre chegadas de dois veículos consecutivos segue uma distribuição
Um estatístico utilizou uma amostragem aleatória estratificada sobre uma população que se divide nos estratos A e B, de tamanhos NA = 20 mil e NB = 30 mil, respectivamente. Sabe-se que as variâncias da variável de interesse dentro desses estratos são, respectivamente, SA = 9 e SB = 4. O estatístico retirou uma amostra aleatória de tamanho n = 500, de acordo com a alocação ótima de Neyman. Com base nessas informações, assinale a opção correspondente às quantidades observadas pelo estatístico nos estratos A e B, respectivamente.
No modelo de regressão múltipla com variável resposta yi e regressoras xi1, xi2, ..., xip, a estimativa da variância dos erros aleatórios segue a forma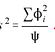
A respeito desse modelo, assinale a opção correta.
O gráfico a seguir apresenta o número de acidentes sofridos pelos empregados de uma empresa nos últimos 12 meses e a frequência relativa.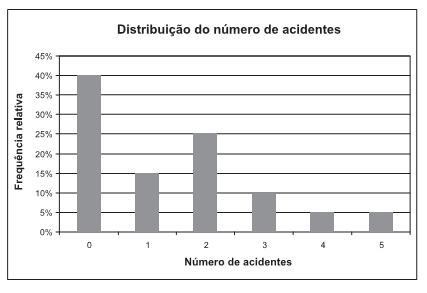
A mediana menos a média do número de acidentes é
Sejam f(k) e g(k), k = 1, 2, ..., respectivamente, a função de autocorrelação parcial e a função de autocorrelação, de um processo ARIMA (p,d,q). Sabendo que g(k) é uma mistura de exponenciais ou ondas senoides amortecidas e que para f(k) somente f(1) e f(2) são diferentes de zero, então:
Uma variável aleatória contínua, X, com distribuição uniforme no intervalo [a,b], a < b, tem média igual à variância de uma variável com distribuição qui-quadrado com 4 graus de liberdade. Se P (X < 1 ) = 1 ⁄ 9 então P (1 < X < 5) é:
Na venda de uma partida de 10.000 peças, o vendedor recebe a seguinte proposta do comprador A: Este examinará uma amostra aleatória de n = 100 peças e pagará R$ 10,00 por peça, se houver até duas defeituosas na amostra e pagará R$ 5,00 por peça, caso contrário. Se 4% de todas as peças são defeituosas, o valor médio que o comprador A se propõe a pagar por peça, calculado quando se faz uso da aproximação de Poisson para as probabilidades necessárias ao cálculo do referido valor médio, é, em reais, igual a 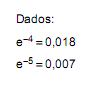
O diâmetro, X, de uma peça tem distribuição normal e deve estar entre 96 mm e 105 mm para passar no controle de qualidade. Sabe-se que 0,6% dos diâmetros das peças ultrapassam o limite superior (105 mm) e que 2,3% são inferiores ao limite inferior (96 mm). A probabilidade de uma peça, selecionada ao acaso, passar no controle de qualidade quando os limites inferior e superior forem alterados para 97 mm e 104 mm, respectivamente, é de
O objetivo de um estudo é verificar a hipótese de igualdade das médias obtidas em um teste aplicado para 5 grupos de trabalhadores, que tiveram treinamentos diferentes, independentemente. Cada grupo foi formado por 10 trabalhadores e a estatística F (F calculado) no quadro de análise de variância foi igual a 3,75. A porcentagem que a fonte de variação entre grupos representa da fonte de variação total é de
Os 10 elementos de uma amostra aleatória correspondentes a uma variável aleatória X apresentaram valores diferentes e foram colocados em ordem crescente. O intervalo de confiança [m,n], em que m é o segundo elemento deste conjunto e n o nono elemento, é um intervalo de confiança da mediana de X. O nível de confiança deste intervalo é de
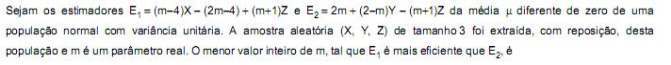
Em um período de 140 dias foi analisado o número de reclamações registradas por dia em um guichê de uma repartição pública. Verificou-se que o número de dias (fi) em que ocorreram i reclamações (0 ≤ i ≤ 6) pode ser obtido pela fórmula: fi = -i2 + 8i +9. A soma dos valores da média aritmética, da mediana e da moda (número de reclamações por dia), é igual a
Em dezembro de 2011 foi realizado um levantamento em uma empresa que proporcionou a tabela de frequências relativas abaixo, referente aos salários de seus empregados, observando que 3m + n = 25%. 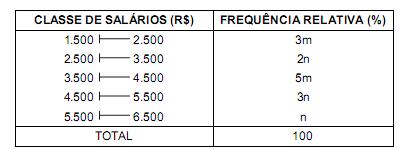
O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio deste intervalo. O valor da mediana (Md) foi obtido pelo método da interpolação linear. Então, tem-se que
Um analista sabe que, para os processos de dotação orçamentária de uma determinada prefeitura, a probabilidade de encontrar alguma irregularidade é de 20%. Presumindo que esses processos são independentes entre si, a probabilidade de que, numa amostra de dez, no máximo dois processos apresentem alguma irregularidade será de:
Seja x1, x2, ..., nn uma amostra aleatória proveniente de uma distribuição de Poisson com parâmetro λ .
Neste caso a distribuição assintótica do estimador de máxima verossimilhança para λ é:


