Considere que a amostra aleatória simples X1, X2, ..., Xn tenha sido
retirada de uma distribuição exponencial com função de densidade
na forma f(x) = γexp(–γx), em que x > 0 e γ > 0. Com relação a essa
amostra e à inferência estatística, julgue os itens que se seguem.
De acordo com o teorema limite central, a soma
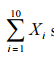
segue uma distribuição normal.
Com referência à estatística computacional, julgue os itens
subsequentes.
O amostrador de Gibbs é um algoritmo que permite gerar amostras de distribuições multivariadas.
No que concerne aos processos estocásticos, julgue os itens
seguintes.
Em um processo de Poisson com média 1, a probabilidade de
não ocorrer nenhum evento até o instante 1 será inferior a
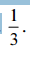
Julgue os itens a seguir, relativos à análise multivariada.
Na análise discriminante por meio do escore de Fisher, convencionou-se que os dados seguem distribuição normal.
Julgue os itens de 96 a 100, relativos à análise de séries temporais.
Se Zt* for o valor de um filtro linear (médias móveis) no instante t e se μt = E(Zt ) for o valor esperado da série no mesmo instante, então E(Zt *) > μt .
Julgue os itens que se seguem, acerca da estatística descritiva.
Na distribuição da quantidade de horas trabalhadas por empregados de certa empresa, é sempre possível determinar a média e a mediana amostral; porém é possível que essa distribuição não possua moda.
Com relação à teoria de probabilidades, julgue os próximos itens.
Com base na distribuição Normal, é correto afirmar que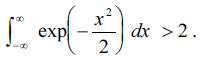 
.
No que se refere a distribuições discretas, julgue os seguintes itens.
Em toda distribuição binomial, a média será menor que a variância.
Com base em distribuições contínuas, julgue os itens subsequentes.
Toda função não negativa é uma densidade de probabilidade.
De acordo com as probabilidades condicionais, julgue os itens que subsecutivos.
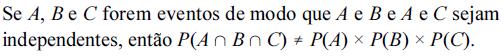
Considerando o conceito de distribuição de probabilidade, julgue os itens de 72 a 78.
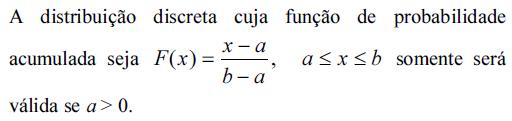
No que concerne a união e intersecção de eventos, julgue os itens que se seguem
Um estudo sobre a informalidade no mercado de trabalho mostrou
que o número X de empregados não registrados por microempresa
segue uma distribuição binomial negativa na forma
P(X = k) = (k + 1)p2(1 p)k, em que k = 0, 1, 2, ... e o parâmetro p
dessa distribuição é tal que 0 < p < 1. Com base nessas informações
e considerando a média amostral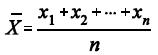 
em que X1, X2, ..., Xn representa uma amostra aleatória simples retirada
dessa distribuição, julgue os itens a seguir.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
Considerando-se o princípio da máxima verossimilhança, infere-se que a estimativa da probabilidade P(Y > 4) é nula.
Considerando que o número mensal Y de acidentes de trabalho siga
uma distribuição de Poisson com média m e que a tabela acima
apresente a realização de uma amostra aleatória simples de tamanho
n = 100, retirada da população Y, julgue os itens subsecutivos.
A estimativa de máxima verossimilhança da probabilidade P(Y = 0) é igual a 0,50.
