O preço de um produto, denotado por Z, é uma composição dos preços de dois elementos que o compõe, denotados por X e Y.
Sabe-se que:
I.Z = 2X + Y
II.A distribuição conjunta de X e Y é dada na tabela a seguir, onde os valores de X e Y são dados em centenas de reais:
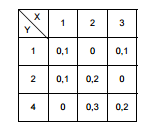
Nessas condições, a probabilidade do produto custar mais do que 500 reais é igual a
Atenção: Para resolver às questões de números 58 a 60, use, dentre as informações abaixo, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:
P(Z < 0,44) = 0,67; P(Z < 0,5) = 0,691; P(Z < 1) = 0,841; P(Z < 1,5) = 0,933; P(Z < 2,05) = 0,98.
A renda média de uma comunidade pode ser considerada como sendo uma variável aleatória com distribuição normal com
média μ reais e desvio padrão de R$ 400,00. Se a porcentagem da população que tem renda superior a R$ 2.000,00 é de 67%,
o valor de μ, em reais, é
A tabela de frequências absolutas abaixo corresponde aos salários dos funcionários de uma empresa pública em março de 2014.
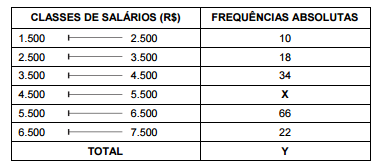
Utilizando o método da interpolação linear, encontra-se que a mediana (Md) dos salários destes funcionários é igual a
R$ 5.260,00. O valor da média aritmética (Me) dos salários é calculado considerando que todos os valores, incluídos num certo
intervalo de classe, são coincidentes com o ponto médio deste intervalo. O valor correspondente da moda (Mo) dos salários,
utilizando a relação de Pearson (Mo = 3xMd - 2xMe), em reais, é igual a
Em uma grande cidade é realizada uma pesquisa com 400 eleitores, escolhidos aleatoriamente, sobre o nível de satisfação do
atual prefeito e 80% deles classificaram como “Bom". Deseja-se construir um intervalo de confiança de 95% para esta proporção
com base neste levantamento supondo que é normal a distribuição amostral da frequência relativa dos eleitores que consideram
o nível de satisfação como “Bom". Dado que na distribuição normal padrão Z as probabilidades P(Z > 1,96) = 0,025,
P(Z > 1,64) = 0,05 e P(Z > 1,28) = 0,10, obtém-se que o intervalo, em %, é igual a
Atenção: Para responder às questões de números 46 e 47, considere os dados abaixo. Um grupo de 400 funcionários de um tribunal apresenta, de acordo com o sexo e a qualificação profissional, a seguinte composição:
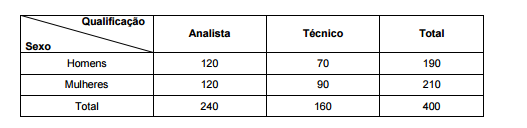
Quatro funcionários, dentre esses 400, serão selecionados ao acaso e com reposição. A probabilidade de que, nessa seleção,
exatamente dois sejam homens e analistas é igual a
Em um departamento de um órgão público existem 80 funcionários. Desse total, 40 são analistas financeiros, 20 são analistas
jurídicos e 20 são técnicos jurídicos. Dentre esses 80 será selecionada uma amostra aleatória de 4 para formar uma comissão.
O número de amostras estratificadas, com alocação proporcional à função exercida, que poder-se-ia realizar é igual a
Atenção: Para responder às questões de números 54 e 55 use, dentre as informações dadas abaixo, as que julgar apropriadas. Se e é a base dos logaritmos naturais, tem-se
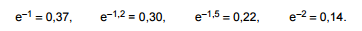
Para fazer uma compra, via internet, uma pessoa escolhe entre duas grandes lojas de departamentos: A e B. Suponha que em
40% dos casos essa pessoa escolha a loja A e em 60% dos casos escolha a B. Suponha que o tempo de conexão, em minutos,
para a efetivação da compra seja uma variável com distribuição exponencial com médias 5 minutos e 4 minutos,
respectivamente, para a compra em A e B. Nessas condições, a probabilidade de ao fazer uma compra a loja escolhida ser B,
dado que o tempo de efetivação da compra foi superior a 6 minutos é igual a
Atenção: Para responder às questões de números 58 a 60 use, dentre as informações dadas abaixo, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:
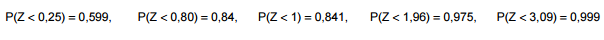
Considere X1, X2, ...Xnn uma amostra aleatória simples, com reposição, da distribuição da variável X, que tem distribuição normal
com média µ e variância 36. Seja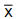 
a média amostral dessa amostra. O valor de n para que a distância entre 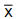e µ seja, no máximo, igual a 0,49, com probabilidade de 95% é igual a
Uma variável aleatória contínua tem a sua função
densidade de probabilidade dada por:
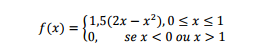
Com base nas informações apresentadas, assinale a
alternativa que indica a 930 ≤ x ≤ 0,54.
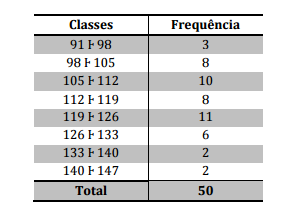
Considerando a distribuição de frequência apresentada,
assinale a alternativa que apresenta a mediana do
conjunto de dados.
Considerando as três distribuições apresentadas a seguir:
I) 0, 5, 6, 7, 7, 7, 7
II) 2, 3, 5, 6, 7, 8, 9
III) 12, 14, 16, 16, 16, 18, 19, 19
Com base nesses dados, assinale a alternativa que indica a
soma da mediana da distribuição I com o quartil inferior
da distribuição II menos o extremo superior da
distribuição III.
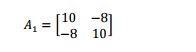
Considerando a matriz de covariâncias amostrais para p =
2 apresentada, assinale a alternativa que corresponde à
variância generalizada da matriz C.
Considere as afirmativas abaixo concernentes á estimação pontual de estimadores
Está correto o que se afirma em
A curva intensidade-duração-frequência (IDF) é obtida a partir da análise estatística de uma série longa de dados. Alternativamente, a intensidade de uma chuva (mm/h), em função do seu tempo de retorno em anos (TR) e da sua duração em minutos (td ), pode ser dada pela equação a seguir:
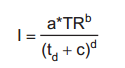
Considere as informações a seguir para responder às questões de n os 55 e 56.
Um feirante possui uma Kombi para transportar caixas de frutas. Em uma viagem, ele consegue transportar no veículo 200 caixas de laranjas - caso transporte apenas laranjas - ou 300 caixas de tangerinas - caso transporte apenas tangerinas. O lucro por caixa de frutas é o seguinte: 20 unidades monetárias pelas laranjas, 30 unidades monetárias pelas tangerinas e 35 unidades monetárias pelas maçãs. De acordo com sua estimativa de vendas, o feirante decide transportar pelo menos 100 unidades de maçãs. Considere a variá- vel X 1 como a quantidade vendida de caixas de maçãs, X2 a de caixas de laranjas e X 3 a de caixas de tangerinas.
Um método utilizado para resolver esse tipo de problema de programação linear inteira é o
