Foi realizado um estudo com o objetivo de avaliar se o tempo que o café moído fica estocado afeta seu aroma. Em cada uma das sessões de avaliação sensorial, duas amostras foram obtidas ao acaso e os avaliadores atribuíram uma pontuação à amostra.
Sejam as variáveis: X = Tempo de Estocagem, Y1 = Pontuação Média da Amostra 1 e Y2 = Pontuação Média da Amostra 2. A matriz de variância e covariância está representada abaixo.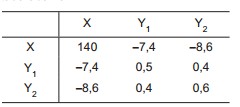
Sendo assim, qual é o coeficiente de correlação, aproximado, entre o X e o Y1?
A tabela de frequências absolutas, abaixo, corresponde à distribuição dos salários dos empregados em uma empresa, em que
todos os intervalos de classe têm a mesma amplitude. O valor da mediana dos salários (obtido por interpolação linear) é igual a
R$ 4.100,00 e pertence ao intervalo [c , d) em que c = R$ 3.500,00.
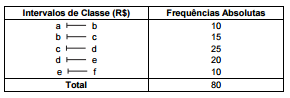
Calculando o valor da média aritmética destes salários, considerando que todos os valores incluídos em um certo intervalo de
classe são coincidentes com o ponto médio deste intervalo, verifica-se que este valor pertence ao intervalo (em R$)
Em um estudo é considerada a distribuição binomial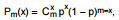 
em que x é o número de ocorrências de um
acontecimento em m provas, sabendo-se que na i-ésima experiência de uma série de n, comportando m provas cada uma, o
acontecimento ocorreu xi
vezes. Deseja-se encontrar, pelo método da máxima verossimilhança, a estimativa pontual do
parâmetro p com a qual um acontecimento A ocorre em cada prova, sabendo-se que em 80 experiências de 5 provas cada uma
forneceram a distribuição abaixo.
O valor da estimativa de p é então, em %, igual a
Um noticiário divulga que o salário médio de uma determinada carreira profissional é de R$ 4.150,00. Como há uma suspeita de
que o salário médio (μ ) desta carreira é superior a R$ 4.150,00, extrai-se uma amostra aleatória da população destes salários de
tamanho igual a 256, detectando uma média igual a R$ 4.180,00. Foram formuladas as hipóteses H0: μ = R$ 4.150,00 (hipótese
nula) e H1: μ > R$ 4.150,00 (hipótese alternativa), considerando que a população é normalmente distribuída e de tamanho
infinito. Considere na curva normal padrão (Z ) as probabilidades P(Z > 2,33) = 0,01 e P(Z > 1,64) = 0,05. Se o desvio padrão
populacional é igual a R$ 225,00, então, com base na amostra, H0
Deseja-se determinar, com a utilização do teste do qui-quadrado, respectivamente ao consumo de um produto em que existem
somente as marcas X, Y e Z se há dependência da escolha da marca do produto com relação à classe do consumidor (A, B ou
C).Uma amostra aleatória de 160 consumidores, em que cada um citou sua preferência por uma e somente uma marca,
forneceu os resultados apresentados na tabela abaixo.
Verifica-se que ao nível de significância α, o valor do qui-quadrado tabelado, com o respectivo número de graus de liberdade, é
inferior ao valor do qui-quadrado observado. Então, considerando o nível de significância α,
O objetivo de um estudo é testar a hipótese de igualdade das médias de um atributo X, a um determinado nível de significância
α, correspondente a 3 grupos I, II e III, independentes, cada um contendo 15 observações obtidas aleatoriamente. Pelo
quadro de análise de variância, observou-se os seguintes resultados com relação às respectivas observações sabendo-se que o
valor da estatística F (F calculado) utilizado para a tomada de decisão é igual a 33,6.
O valor do módulo de (X − Y) é igual a
Um experimento será repetido até que um particular evento A ocorra pela segunda vez. Sabe-se que:
I.Todas as repetições do experimento são independentes.
II.A probabilidade de A ocorrer em cada repetição é igual a p.
III.A variável X que representa o número de repetições do experimento até que A ocorra pela segunda vez tem média 3.
Nessas condições, a probabilidade condicional denotada por P(X = 2|X ≤ 3) é igual a
Sobre análise multivariada, considere:
I.Na análise fatorial nenhuma variável é definida como dependente ou independente.
II.Na análise de agrupamentos deve haver bastante homogeneidade interna (dentro do agrupamento) em cada um dos
agrupamentos resultantes.
III.Na análise de correlação canônica o princípio subjacente é desenvolver uma combinação linear de cada conjunto de
variáveis dependentes e independentes para minimizar a correlação entre esses dois conjuntos.
IV.O escalamento multidimensional é uma técnica multivariada apropriada para representar n elementos em um espaço
dimensional menor que o original, levando em consideração a similaridade que os elementos têm entre si.
Está correto o que consta APENAS em
A função densidade de probabilidade da variável bidimensional contínua (X,Y) é dada por:
Onde K é a constante adequada para tornar f(x) uma função densidade de probabilidade.
Nessas condições, a esperança condicional de X, dado que Y é igual a 1/6, denotada por E (X|Y = 1/6), é igual a
Atenção: Para resolver às questões de números 58 a 60, use, dentre as informações abaixo, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:
P(Z < 0,44) = 0,67; P(Z < 0,5) = 0,691; P(Z < 1) = 0,841; P(Z < 1,5) = 0,933; P(Z < 2,05) = 0,98.
Uma máquina enche pacotes de um determinado cereal com um peso que pode ser considerado como uma variável aleatória X
com média 250 g e desvio padrão de 12 g. Uma amostra aleatória, com reposição, de n pacotes é sorteada da produção da
máquina. Seja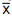 
a média amostral dessa amostra. O valor de n para que 
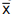não difira da sua média por mais do que 4,1 g, com probabilidade de 96%, é igual a
Seja { X1, X2, X3, ... , X80 } uma população constituída de 80 números estritamente positivos, sabendo-se que a média aritmética
e o desvio padrão desta população são, respectivamente iguais a 20 e 15. Resolve-se excluir desta população 30 números, cuja
soma de seus quadrados é igual a 12.000, formando uma nova população e o novo valor da variância passa a ter o valor de 436.
O correspondente novo valor da média aritmética da nova população apresenta um valor igual a
A classe de estimadores não viesados E = 2(m - 1)X - (m - 1)Y + nZ , sendo m e n parâmetros reais, é utilizada para estimar a
média µ de uma população normal com variância unitária. Sabe-se que (X, Y, Z) é uma amostra aleatória extraída, com
reposição, desta população. A variância do estimador mais eficiente, entre os estimadores desta classe, verifica-se para m
igual a
Em uma empresa foram selecionados aleatoriamente 256 empregados que se submeteram a um treinamento durante 30 dias.
Verificando que x empregados apresentaram melhora no desempenho após o treinamento, decidiu-se utilizar o teste do sinal,
atribuindo x sinais positivos para os empregados que melhoraram e (256 - x) sinais negativos para os restantes. Aplicando
então o teste do sinal para decidir se a proporção populacional de sinais positivos (p) é igual a 50%, a um nível de significância
de 5%, foram formuladas as hipóteses H0 : p = 50% (hipótese nula) contra H1 : p ? 50% (hipótese alternativa). Com a
aproximação da distribuição binomial pela normal, sem a correção de continuidade, foi apurado o valor do escore reduzido r
correspondente para comparação com o valor crítico z da distribuição normal padrão Z tal que a probabilidade
P(|Z|≤z ) = 95% . Se r = 2,5, então x é igual a
Atenção: Para responder às questões de números 42 e 43, considere o texto abaixo. Uma empresa decide utilizar o modelo linear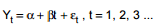 
para prever o volume de vendas (Yt ), em milhões de reais, no ano (2002 + t). Os parâmetros α e β são desconhecidos e εt corresponde ao erro aleatório com as respectivas hipóteses do modelo de regressão linear simples. Com base nas informações de 2003 até 2012 e utilizando o método dos mínimos quadrados obteve-se as estimativas de α e β. Observação: 
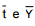correspondem às médias de t e Y no período considerado e seus valores são 5,5 e 20, respectivamente.
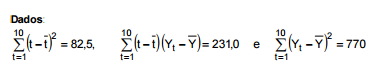
Utilizando a equação da reta obtida pelo método dos mínimos quadrados e calculando as previsões para 2013 e 2018, observa-se
que o valor da previsão para 2018 supera o valor da previsão para 2013 em, milhões de reais,
Cada ensaio de um determinado experimento aleatório pode resultar em sucesso com probabilidade 0,4 ou fracasso com
probabilidade 0,6. Seja X a variável aleatória que representa o número de ensaios, desse tipo, independentes, até a ocorrência
do primeiro sucesso. Baseado em X, o seguinte jogo foi proposto a um jogador que irá participar do experimento: ganha 20 reais
se X assumir o valor 3, perde 5 reais se X assumir o valor 2 e não ganha nada se X assumir qualquer valor diferente de 2 ou 3.
Se o jogador paga K reais para participar desse jogo, o valor de K para que o lucro médio do jogador seja igual a zero é, em
reais, igual a
