Um estudo, realizado por determinado sindicato de trabalhadores, teve por objetivo verificar a associação entre duas variáveis: X e Y. Sabe−se que:
1- X representa a variável posição em relação a determinado projeto sindical com 3 respostas possíveis: Favoráveis (F),
Desfavoráveis &$40;D) e Indecisos &$40;I).
2- Y representa a variável sexo com 2 respostas possíveis: Homens &$40;H) e Mulheres&$40;M).
Na população dos sindicalizados, tem−se que a proporção de
I. Homens é de 40% e a de Mulheres é de 60%.
II. Favoráveis é de 50%, a de Desfavoráveis é de 40% e a de Indecisos é de 10%.
III. Indecisos entre os Homens é de 20%.
IV. Mulheres entre os Desfavoráveis é de 40%.
Dois sindicalizados foram selecionados aleatoriamente, com reposição, dentre os elementos dessa população. A probabilidade
de, nessa amostra, exatamente um ser do sexo feminino (M) e ser favorável (F) à proposta sindical é, em porcentagem, igual a
A função geratriz de momentos da variável aleatória X é dada por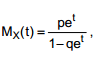 
onde p é o parâmetro do modelo, p + q = 1 e 0
A quantia (em milhões de reais) gasta anualmente em suprimentos de papelaria em um determinado órgão governamental é uma
variável aleatória X com função densidade de probabilidade dada por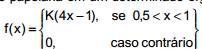
, onde K é uma constante
a propriada para garantir que f (x) seja uma função densidade de probabilidade. Nessas condições o valor de K é igual a
Atenção: Para responder às questões de números 38 a 40 use, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z < 0,30) = 0,62, P(Z < 1,04) = 0,85, P(Z < 1,20) = 0,88, P(Z < 1,28) = 0,90,
P(Z < 1,64) = 0,95, P(Z < 2) = 0,98,
Sabe−se que o vetor aleatório t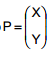
em distribuição normal bivariada com vetor de médias 
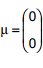e matriz de covariâncias
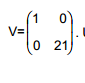Uma amostra aleatória [(X1,Y1),...(Xn,Yn )], simples, com reposição de tamanho n é selecionada da distribuição de P.
Considere a variável aleatória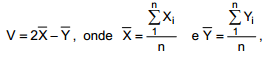 
são as respectivas médias amostrais de X e Y.
Nessas condições se P(|V| < 0,32) = 0,80 , o valor de n é
Atenção: Para responder às questões de números 38 a 40 use, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z < 0,30) = 0,62, P(Z < 1,04) = 0,85, P(Z < 1,20) = 0,88, P(Z < 1,28) = 0,90,
P(Z < 1,64) = 0,95, P(Z < 2) = 0,98,
Suponha que uma instituição financeira criou um fundo de investimento onde o ativo é aplicado em uma combinação de Letras
de Câmbio do Agronegócio − LCA com Letras de Câmbio Imobiliárias − LCI. Supondo−se que a variável L que representa o lucro
mensal do fundo, em milhares de reais (MR), seja dada por: L = AX, sendo A o vetor de constantes dado por A = (2 1) e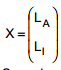 
o vetor de variáveis aleatórias, onde LA e LI representam, respectivamente, os lucros mensais das letras LCA e LCI.
Suponha que LA tem distribuição normal com média 80MR e desvio padrão 3MR; que LI tem distribuição normal com média
70MR e desvio padrão de 8MR e que essas duas variáveis são independentes. Nessas condições, a probabilidade do lucro
mensal de tal investimento ser um valor no intervalo (233MR ; 242MR) é igual a
Sejam duas variáveis X e Y representando os salários dos empregados nas empresas Alfa e Beta, respectivamente, com 100 empregados cada uma. Em um censo realizado nas duas empresas apurou−se que a média, em milhares de reais, de X foi igual a 2,5 e a média de Y foi igual a 3,2. A soma dos valores dos quadrados, em (R$ 1.000,00)2, de todos os valores de X foi igual a 650 e de todos os valores de Y foi igual a 1.047,04. Assim, o coeficiente de variação de
Uma amostra aleatória de tamanho 9 foi extraída de uma população com função densidade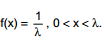 
Sabendo−se que
o menor valor da amostra foi igual a 3 e o maior valor igual a 15, obteve−se pelo método da máxima verossimilhança, com base
nos dados da amostra, a estimativa pontual para a média e a variância da população. A variância apresenta um valor igual a
Em um determinado ramo de atividade, a população de todos os salários dos empregados é considerada normal e de tamanho infinito. O desvio padrão populacional apresenta um valor igual a R$ 200,00. Deseja−se testar a hipótese H0: = μ = R$ 1.700,00 (hipótese nula) contra H1: μ ≠ R$ 1.700,00 (hipótese alternativa) com base em uma amostra aleatória de tamanho 64 extraída da população (µ é a média da população). A média encontrada para esta amostra apresentou um valor igual a M reais. Fixando o nível de significância do teste em 5% e considerando que na curva normal padrão (Z) as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05, H0 não será rejeitada caso
O objetivo de um estudo consistia em deduzir a relação entre uma variável X e uma outra variável Y por meio de um modelo
linear simples Yi = α + βXi + βi , em que i é a i−ésima observação, α e β são parâmetros desconhecidos e εi é o erro aleatório com
as respectivas hipóteses consideradas para a regressão linear simples. As estimativas de α e β foram obtidas pelo método dos
mínimos quadrados com base em 20 observações (Xi, Yi), notando que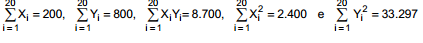
Utilizando o teste t de Student para testar a existência da regressão a um determinado nível de significância, em que foram
formuladas as hipóteses H0: β = 0 (hipótese nula) e H1: β ≠ 0 (hipótese alternativa), obtém−se que o valor do t calculado para ser
comparado com o t tabelado, levando em conta os respectivos graus de liberdade, é
Em 10 grandes empresas foram escolhidos aleatoriamente em cada uma 5 empregados para realizar uma determinada tarefa, independentemente, sendo anotado o tempo em horas que cada empregado demorou para realizar a tarefa. Deseja−se saber, a um determinado nível de significância, se os tempos médios das empresas para a realização da tarefa são iguais. Pelo quadro de análise de variância, a soma de quadrados, devido à fonte de variação total, é igual a 1.400 e o valor da estatística F (F calculado), utilizado para testar a igualdade dos tempos médios entre as empresas, apresentou um valor igual a 15. Neste quadro, o correspondente valor da soma de quadrados entre empresas é igual a
A variância de um conjunto de dados é 4 m2.
Para o mesmo conjunto de dados foram tomadas mais duas medidas de variabilidade:
a diferença entre o terceiro e o primeiro quartil e o coeficiente de variação.
Esses dois valores caracterizam-se, respectivamente, por
Seja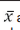 
a média amostral de uma variável aleatória de
tamanho de uma população com variância
conhecida σ2 . O intervalo de confiança de
para média é dado por:
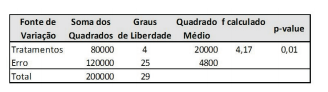
Observando a tabela abaixo para uma análise de
variância ANOVA simples, o que se pode concluir a
respeito das seguintes hipóteses?
H0= média dos tratamentos são iguais
H1= pelo menos duas médias não são iguais
