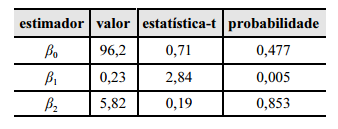
A tabela a seguir apresenta o resultado da estimação pelo método dos mínimos quadrados ordinários do modelo
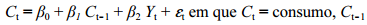consumo defasado em um período, Y
t = renda, gt = resíduo e β0, β1 e β2 são os coeficientes de regressão múltipla.
Número de observações: 154
R-quadrado: 0,051
estatística F: 4,04
valor-p (estatística F): 0,02
Com base nessas informações, julgue os itens subsecutivos
De acordo com a estatística do R-quadrado, 5,1% da variação total do consumo é explicada pelo modelo econométrico.
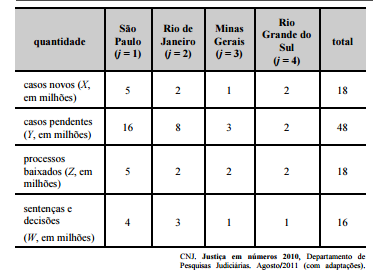
O quadro acima mostra uma síntese da movimentação processual
dos tribunais de justiça dos estados de São Paulo, Rio de Janeiro,
Minas Gerais, Rio Grande do Sul e do total da justiça estadual no
Brasil em 2010. Considere que o estoque de processos em
andamento no estado j (Ej), no final de 2010, seja um indicador que
se define como Ej= Xj+ Yj – Zj – Wj , em que j = 1, 2, ..., 27; Xj
representa o número de casos novos registrados em 2010 no
estado j; Yj seja a quantidade de casos pendentes no estado j (i.e.,
casos anteriores que não foram solucionados até o final de 2010);Zj denota o total de processos baixados (arquivados) no estado j
durante 2010 e Wj seja o número de sentenças e decisões proferidas
no estado j até o final de 2010. Considere, por fim, que, para todos
os efeitos, o Distrito Federal seja um estado. Com base nessas
informações e no quadro acima, julgue os itens que se seguem.
O estoque de processos em andamento no estado de São Paulo
no final de 2010 representou 37,5% do total dos estoques de
processos em andamento nos tribunais estaduais do país nesse
mesmo período.
Nas estatísticas do Poder Judiciário, a taxa de
congestionamento (X), que consiste em um indicador que permite
medir a efetividade da movimentação processual de um tribunal, é
uma variável aleatória contínua com função de densidade
f(x) expressa por
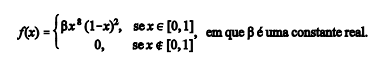
Com base nessas informações, julgue os próximos itens.
A distribuição da taxa de congestionamento X é simétrica em
torno de 0,5.
Considerando A e B dois eventos aleatórios, com probabilidades
P(A) = 0,4 e P(B) = 0,1, e o evento complementar Bc, julgue os
itens seguintes, relativos a probabilidade condicional.
Considerando–se que A e B sejam eventos mutuamente
excludentes, é correto afirmar que P(A|Bc) = 0.
O núcleo de assistência jurídica de um fórum que presta
assistência jurídica gratuita a pessoas carentes recebe diariamente
X casos novos, conforme uma distribuição condicional na forma
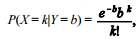em que k = 0, 1, 2, ..., b > 0 e Y segue uma
distribuição exponencial com função de densidade f(y) = 2e–2y , em que y > 0.
Considerando essa situação hipotética, julgue os itens subsequentes
Considerando essa situação hipotética, julgue os itens subsequentes.
Considerando–se que, em certo dia, o núcleo tenha recebido 5
casos novos, é correto afirmar que a distribuição condicional
Y|X = 5 segue a distribuição gamma na forma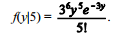 
.
Considerando que X seja uma variável aleatória contínua, tal que
E(X) = 1 e E(X2) = 4, julgue os itens seguintes.
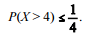
Considerando X1, X2, ..., Xn uma amostra aleatória simples retirada
de uma distribuição com média μ e desvio padrão σ,
e a estatística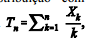
julgue os itens que se seguem.
Se 
então é um estimador não tendencioso (ou não viciado) da média amostral.
Com o propósito de produzir inferências acerca da
proporção populacional (p) de pessoas satisfeitas com determinado
serviço oferecido pelo judiciário brasileiro, foi considerada uma
pequena amostra de 30 pessoas, tendo cada uma de responder 1,
para o caso de estar satisfeita, ou 0, para o caso de não estar
satisfeita. Os dados da amostra estão registrados a seguir.
0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1
Com base nessas informações, julgue os itens seguintes.
Considerando que Z represente a distribuição normal padrão,
que P(Z > 2) ≅ 0,975 e P(Z > 1,645) = 0,95 e que 2,51 é valor
aproximado para √63 é correto afirmar que o intervalo [a; b]
que representa um intervalo de 95% de confiança para a
proporção de pessoas não satisfeitas está contido no intervalo
[0,4; 0,9].
Segundo notícia veiculada recentemente, em rede nacional,
os processos do judiciário estão demorando mais que o razoável
porque os juízes têm de analisar, em média, 3 mil processos por
ano. Para verificar o fato, um analista coletou a quantidade de
processos de uma amostra de 10 juízes, estando os resultados
dispostos a seguir (em mil processos por ano).
2 5 4 3 2 2 3 3,5 2,5 5
Com base nessas informações e considerando que μ representa a
média populacional por juiz, julgue os itens subsequentes.
Se o objetivo fosse apenas verificar a veracidade da afirmação
de que os juízes analisam em média 3 mil processos por ano,
então a hipótese nula seria do tipo bilateral, isto é,
H0: μ ≠ 3 mil.
Para verificar se a escolaridade dos servidores de
determinado tribunal estaria relacionada à eficiência no atendimento
ao público, um analista pesquisou alguns servidores, dispondo as
informações obtidas na tabela a seguir.
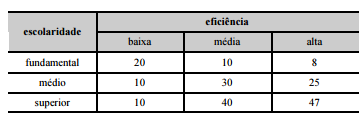
Com base nessas informações e considerando que a escolaridade de
cada servidor entrevistado, apresentada na tabela, corresponda à
maior escolaridade que possui, julgue os itens seguintes.
Considere que os níveis críticos da distribuição qui–quadrado
com 1 a 4 graus de liberdade sejam, respectivamente
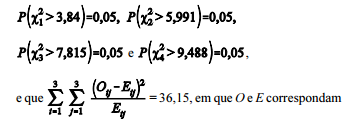
, às contagens observadas e esperadas. Nesse caso, é correto
afirmar, com 5% de significância, que não há evidências
estatísticas que permitam rejeitar a hipótese de independência.
O administrador de uma organização, antes de promover
um processo de treinamento de pessoal, fez um treinamento piloto
com 10 empregados para verificar a eficácia da metodologia
aplicada no treinamento. A tabela a seguir mostra a quantidade de
processos resolvidos por cada um desses 10 empregados,
numerados de 1 a 10, no mês anterior ao treinamento piloto e no
mês seguinte.
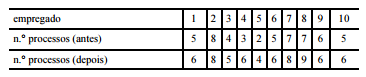
Considerando as informações acima e que os dados da tabela
seguem uma distribuição normal, julgue os itens subsequentes.
O teste a ser aplicado possui 18 graus de liberdade.
Com relação aos modelos de regressão, julgue os itens
subsecutivos.
Em um modelo de regressão linear, a variância associada às
estimativas obtidas pelo método da máxima verossimilhança é
menor que as variâncias associadas às estimativas obtidas por
mínimos quadrados.
Com relação à inferência para os parâmetros de modelos de
regressão linear, julgue os seguintes itens.
Julgue os próximos itens, referentes à qualidade de ajuste de um
modelo de regressão.
Se um modelo de regressão linear simples tivesse coeficiente
de determinação igual a 0,75, então, nesse modelo, a soma de
quadrados do resíduo seria menor que a metade da soma de
quadrados totais.
Com relação às técnicas de amostragem, julgue os itens
subsequentes.
Considere que determinado tribunal pretenda avaliar a
proporção de habitantes de um município que foram vítimas
de algum tipo de violência e que não exista um banco de dados
com a identificação dos habitantes desse município. Nesse
caso, a aplicação da amostragem aleatória simples não será
adequada para selecionar os habitantes do município.
