Julgue os próximos itens, referentes à qualidade de ajuste de um
modelo de regressão.
Considere que um conjunto de dados usado para o ajuste de
um modelo de regressão linear simples tenha a variância da
resposta igual a 4 vezes a variância da variável explicativa.
Nesse caso, se o coeficiente de determinação for igual a 0,95,
então o coeficiente de inclinação da reta de regressão será
menor que 3,5.
Com relação à análise de regressão linear, julgue os itens que se
seguem.
A homocedasticidade é a propriedade conforme a qual o
resíduo de um modelo de regressão tem média 0.
Com relação às técnicas de amostragem, julgue os itens
subsequentes.
Na amostragem aleatória simples sem reposição (AASs), o
tamanho amostral n é calculado por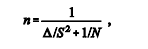
em que N é o tamanho da população, S2 é a variância amostral
e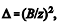 
sendo B o erro máximo de estimação e z o quantil
da distribuição normal. Dessa forma, é correto afirmar que o
maior tamanho amostral na AASs será menor que N.
Julgue os próximos itens, considerando os conectivos lógicos usuais
¬, ∧, ∨, →, ↔ e que P, Q e R representam proposições lógicas
simples.
A proposição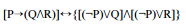
é uma tautologia.
O histograma, abaixo, refere-se à distribuição dos salários dos funcionários lotados em um setor de um órgão público. No eixo
das abscissas constam os intervalos de classe em R$ (todos fechados à esquerda e abertos à direita) e no eixo das ordenadas
as respectivas densidades de frequências em (R$)-1. Define-se densidade de frequência de um intervalo como sendo o
resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.
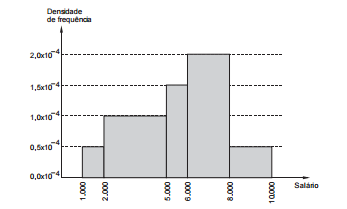
Se o número de funcionários que tem um salário inferior a R$ 5.000,00 é igual a 56, então verifica-se que o número de
funcionários que tem um salário igual ou superior a R$ 2.000,00 e inferior a R$ 8.000,00 é igual a
Suponha que uma variável aleatória X é uniformemente distribuída no intervalo (a , b), em que nem a nem b são conhecidos.
Utilizando o método dos momentos, com base em uma amostra de tamanho 10, obtiveram-se os valores 1 e 4 para a e b,
respectivamente. O valor do momento de ordem 2, centrado na origem, correspondente aos elementos da amostra é
Pretende-se decidir, a um determinado nível de significância, se 5 amostras aleatórias independentes, formando 5 grupos,
provêm de populações com médias iguais por meio do teste de Kruskal-Wallis. Com relação a este teste,
Atenção: Para responder às questões de números 36 e 37, considere a informação abaixo.
A equação da reta y = a + bx foi obtida pelo método dos mínimos quadrados, com base em 10 observações (xi , yi ), i = 1, 2, 3, ...,10, em que foi dotado o modelo linear y i = α + βxi + εi . As estimativas de α e β são respectivamente a e b, i corresponde a i-ésima observação e εi é o erro aleatório com as correspondentes hipóteses do modelo linear simples. Sabe-se que a reta determinada pela equação acima passa pelos pontos ( 20 , 40 ) e ( 100 , 20 ).
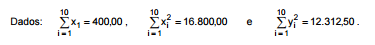
O coeficiente de explicação (R²), definido como sendo o resultado da divisão da variação explicada pela variação total é, em %,
igual a
Suponha que o número de processos trabalhistas que chegam, por dia, a um determinado tribunal regional do trabalho seja uma
variável aleatória com distribuição de Poisson com média igual a λ. Sabe-se que a probabilidade de chegarem 2 processos por
dia é igual a oito vezes a probabilidade de não chegar nenhum. Nessas condições, a probabilidade de, em um determinado dia,
chegarem pelo menos 2 processos é igual a
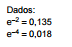
A função geratriz de momentos da variável aleatória X tem a forma: M(t) = (0,2 + 0,8et ) 10.
Nessas condições, a média da variável aleatória Y = 0,5X + 2 é igual a
Sabe-se que a variável aleatória contínua X tem função densidade de probabilidade dada por:
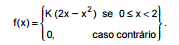
Onde K é a constante adequada para tornar f(x) uma função densidade de probabilidade.
Sejam: μ e θ, respectivamente, a média e a mediana de X. Nessas condições, μ + 2θ é igual a
O diâmetro de uma peça, em dm, é uma variável aleatória contínua X com função de distribuição acumulada dada por:
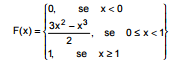
A média aritmética dos salários, em março de 2014, dos empregados em uma empresa é igual a R$ 2.500,00 com um
coeficiente de variação igual a 9,6%. Decide-se aumentar os salários de todos os empregados, tendo que escolher uma entre as
duas opções abaixo:
Opção I: Reajuste de todos os salários, em março de 2014, em 10% mais um abono fixo de R$ 250,00 para todos os salários.
Opção II: Reajuste de todos os salários, em março de 2014, em x% mais um abono fixo de R$ 200,00 para todos os salários.
Existe um valor para x tal que se for escolhida a opção II, a nova média aritmética passa a ser igual à nova média aritmética
caso fosse escolhida a opção I. Nesta situação, o novo coeficiente de variação com a escolha da opção II passa a ser de
Considere que o número de peças (x) que se danificam num recipiente, com 5 peças cada um, durante o transporte obedece a
uma função com densidade f(x) = λe -λx ( x = 0 ) . Verificando aleatoriamente 80 transportes, obteve-se a tabela abaixo.
Avaliando pelo método dos momentos o parâmetro ?, com base nos dados da tabela, encontra-se que a estimativa pontual
deste parâmetro é igual a
Para testar a existência da regressão por meio do teste t de Student, considerando as hipóteses H0 : ß = 0 (hipótese nula) e
H1 : ß ≠ 0 (hipótese alternativa), obtém-se que o correspondente valor da estatística t (t calculado), para ser comparado com o
respectivo t tabelado, pertence ao intervalo
