Considere a seguinte rota fornecida por um aplicativo de celular entre os pontos A e B:
- Siga 1 quilômetro em linha reta.
- Vire à direita, siga mais um quilômetro em linha reta.
- Vire à esquerda, siga 2 quilômetros em linha reta.
- Vire à direita, siga 2 quilômetros em linha reta.
- Você chegou a seu destino.
Considerando que todas as curvas são ângulos de 90°, assinale a alternativa que indica a distância em linha reta entre os pontos A e B:
Ao longo de um mês, o preço inicial P de um produto passou pelas seguintes alterações (sempre em relação ao preço imediatamente anterior):
- Aumento de 20%.
- Redução de 15%.
- Aumento de 10%.
Assinale a alternativa que indica o preço final do produto em relação ao inicial P:
A Etnomatemática pode ser considerada uma abordagem histórico-cultural da disciplina, na qual a matemática deve ser compreendida não apenas como uma constituição social, mas também como uma construção histórica e política. Analise as seguintes afirmações acerca da Etnomatemática:
I. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
II. a Etnomatemática não se trata de um método de ensino nem de uma nova ciência, mas de uma proposta educacional que estimula o desenvolvimento da criatividade, conduzindo a novas formas de relações interculturais.
III. A Etnomatemática trata-se de uma vertente que busca identificar manifestações matemáticas nas culturas periféricas e tem como referências categorias própria de cada cultura.
Assinale a alternativa que indica quais destas afirmações estão corretas:
Dada a matriz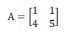 
, assinale a alternativa que indica corretamente a matriz inversa de A:
Analise as quatro afirmações abaixo sobre funções matemáticas:
I. Uma função é injetora se cada elemento do domínio da função possui uma imagem diferente no contradomínio.
II. Uma função é sobrejetora se cada elemento do contradomínio for imagem de um elemento do domínio da função.
III. Uma função não pode ser injetora e sobrejetora simultaneamente.
IV. O contradomínio de uma função numérica sempre será um conjunto numérico maior que o domínio da mesma: por exemplo, se o domínio de uma função for os números naturais, o contradomínio será, no mínimo, o conjunto dos números inteiros.
Assinale a alternativa que indica quais destas afirmações estão corretas:
Considere as duas equações de retas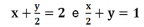 
. Assinale a alternativa correta acerca da relação entre estas duas retas.
Considere três conjuntos finitos A, B, C. A tabela abaixo indica quantos elementos existem em cada conjunto e em suas intercessões. Assinale a alternativa que indica a quantidade de elementos em A ∪ B ∪ C.
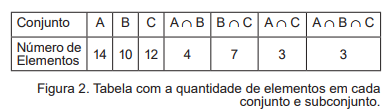
Considere a função f(x) = 2x · (x2 + 4x -5). Assinale a alternativa que indica o valor da soma dos zeros da função, ou seja, onde a função se anula.
No contexto da Aritmética, a divisão de um valor não nulo por zero é considerada indefinida. Abaixo seguem alguns argumentos, utilizando os números naturais, apresentados por um professor a seus alunos, para demonstrar que essa divisão seria indefinida:
I. Ao se dividir objetos entre pessoas, como se atribuir algo a nenhuma pessoa? Por exemplo, ao se dividir seis doces entre duas crianças cada uma receberia três doces; quantos doces seriam dados a cada pessoa se não houvesse nenhuma pessoa?
II. A divisão por zero iria fazer com que falsas igualdades fossem criadas. Por exemplo, 2 · 0 = 3 · 0. Se dividirmos ambos os lados por zero, teríamos 2 =3.
III. A divisão com resto pode ser considerada como uma sequência de subtrações: subtrai-se o divisor do dividendo sucessivas vezes até atingir um número menor que o divisor. Por exemplo, ao dividir 7 por 3, subtraímos 3 duas vezes de 7 até chegar em 1; assim o quociente é 2 e o resto é 1. Se subtrairmos zero, nunca seria atingido um número menor que o divisor.
Porém, parte destes argumentos pode levar, erroneamente, à conclusão que ao se dividir um número qualquer não nulo por zero também resultaria em zero. Assinale a alternativa que indica quais destes argumentos podem levar a esta conclusão equivocada.
Considere as matrizes 
, x ∈ R. Assinale a alternativa que indica o valor correto do determinante do produto A · B.
Um retângulo possui lados de tamanhos diferentes L1 e L2, L1 < L2. Ao triplicarmos o lado menor, teremos um retângulo de lados 3L1 e L2, 3L1 > L2. Qual precisa ser a relação entre L1 e L2 para que o retângulo maior tenha a mesma razão entre os lados que o retângulo menor, ou seja,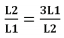
?
João fez uma aposta com Maria da seguinte forma: ele escolherá cinco números inteiros diferentes, de 1 a 10; em seguida, sortearão três números diferentes destes dez números. Se os três números sorteados estiverem dentre os escolhidos por João ele vence, caso contrário, Maria vence. Assinale a alternativa que indica a probabilidade de Maria vencer a aposta.
O décimo-sétimo termo de uma progressão aritmética de razão r =1,5 é 35. Assinale a alternativa que indica o correto valor do sexto termo desta progressão:
Na Ciência da Computação, o prefixo quilo não corresponde a 1.000 vezes, mas sim a 210 vezes; da mesma forma, mega não significa 1.000.000, mas sim 2 20. Assinale a alternativa que indica quantos bytes a mais um megabyte possui em relação ao que teria se o prefixo mega tivesse o valor usual.
Considere a função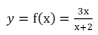 
, para x ≠ 2. Assinale a alternativa que apresenta a função g(y) que é a função inversa de f(x).
