Na figura a seguir, temos a representação de uma transformação T no plano, de polígonos localizados nos 1º e 2º quadrantes em polígonos localizados nos 3º e 4º quadrantes. A transformação gera polígonos semelhantes aos iniciais.

A matriz de transformação correspondente a T é
Considere a representação gráfica das funções f(x)=x2-4x e g(x)=2x-x2 no mesmo sistema cartesioano ortogonal.
A medida da área do plano delimitada pelas funções f e g é um número
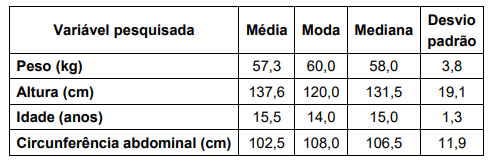
Uma pesquisa foi realizada com um grupo de estudantes de uma turma, durante a aula de Educação Física. Os dados obtidos foram tratados e os resultados estão apresentados na tabela a seguir:
Com as informações da tabela, podemos afirmar que a variável que apresenta o comportamento mais homogêneo é o(a)
Uma logomarca é formada por quatro semicircunferências, duas a duas concêntricas: c1 e c3, c2 e c4. As semicircunferências c1 e c2 têm raio R. A distância entre as semicircunferências concêntricas mede d.

Considere que o comprimento da semicircunferência
c1 é 
A medida da área da região sombreada, em m2, é
Um restaurante possui dois tipos de embalagens de entrega de seus produtos, em forma de tronco de pirâmide de base quadrada: a executiva e a padrão.
Na embalagem padrão, as medidas das dimensões das bases superior e inferior são 20% maiores do que, respectivamente, as medidas das dimensões das bases superior e inferior na embalagem executiva. Além disso, o volume da embalagem padrão é 50% maior que o volume da embalagem executiva.
A razão entre a altura da embalagem executiva e a altura da embalagem padrão é
Chama-se número afortunado Q a todo número primo que é resultado da expressão
Na imagem a seguir (fora de escala) estão representados, em um memo plano, os semicírculos de raios 

O problema a seguir explora uma ideia recorrente no estudo de processos de contagem:
Em um grupo de 3 professores e 8 estudantes, deseja-se formar comissões de 5 pessoas. Quantas comissões podem ser formadas com pelo menos um professor?
Um estudante selecionou um dentre os três professores e, a seguir, quatro dentre as 10 pessoas restantes. A resposta que apresentou foi 3 ∙
Considere a expressão
O valor de S é igual a
O valor de
A respeito da função real definida por
Um ponto P(x, y) é escolhido aleatoriamente no círculo de raio 1, centrado na origem.
Seja R a região definida por R = {(x, y) ∈ IR2,|x − y| ≤ 1}.
A probabilidade de o ponto P pertencer à região R é
Seja VABCD uma pirâmide de vértice V(1, 9, ‒1) e cuja base ABCD é um quadrado situado no plano α de equação x + 2y + 2z ‒ 5 = 0. Sabe-se ainda que A(1,1,1) e B(3, 2, ‒1) são vértices consecutivos dessa base.
O volume dessa pirâmide mede
Um ponto móvel P, que se encontra na origem de um sistema cartesiano ortogonal, começa a realizar um deslocamento, movendo-se de acordo com os passos descritos a seguir:
Sabe-se que esse processo de deslocamento continua indefinidamente, seguindo sempre um padrão no deslocamento norte-sul e, também, um outro padrão no deslocamento leste-oeste. Desta forma, o ponto P se aproxima, cada vez mais, de um ponto fixo T desse mesmo sistema cartesiano ortogonal.
A distância, em unidades, do ponto fixo T à origem desse sistema cartesiano ortogonal é de
Certo experimento foi realizado por um cientista com dois grupos distintos de bactérias, denominadas, respectivamente, X e Y. O objetivo era identificar se algum dos grupos atingiria o total mínimo de 1000 exemplares (bactérias) ao final de dez dias de experimento. Para tal, o cientista foi anotando em uma tabela o total de novas bactérias que surgiam em cada grupo, ao final de cada dia da experimentação. Parte dessa tabela está representada a seguir:
Sabendo que, durante todo o tempo do experimento, nenhuma bactéria morreu e o crescimento de cada grupo de bactérias seguiu sempre o mesmo padrão, é correto afirmar que, ao final do décimo dia, o total mínimo de 1000 bactérias