Observe a tabela-verdade a seguir, na qual P, Q e R são proposições.
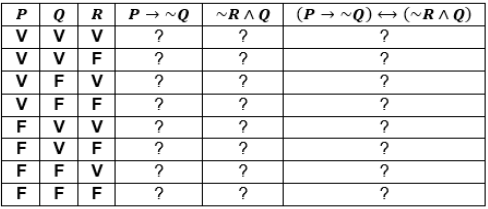
Ao se trocar corretamente todos os símbolos de interrogação pelos valores lógicos V (verdadeiro) ou F (falso), o número de valores lógicos F obtido nas três últimas colunas da tabela é igual a:
Ao se trocar corretamente todos os símbolos de interrogação pelos valores lógicos V (verdadeiro) ou F (falso), o número de valores lógicos F obtido nas três últimas colunas da tabela é igual a:
Considere-se que um grupo de 50 servidores de um tribunal tenha sido selecionado para realizar cursos de aperfeiçoamento e que cada
pessoa desse grupo faça pelo menos um dos seguintes dois cursos: gestão de projetos e ciência de dados.
Nessa situação hipotética, se 29 pessoas fizerem ambos os cursos e 37 pessoas fizerem pelo menos o curso de gestão de projetos, o número exato de pessoas que farão apenas o curso de ciência de dados é igual a
Meire, Ana e Rita, não têm a mesma idade, moram em
cidades distintas, sendo Santo André, São Bernardo e
São Caetano, e cada uma tem um passatempo predileto,
sendo correr, ler ou nadar, não necessariamente nessas
ordens. Sabe-se que: Rita mora em Santo André e gos-
ta de correr; Meire tem mais idade que Ana e que Rita;
quem mora em São Bernardo é mais nova que Rita e
gosta de nadar. Com essas informações, assinale a alter-
nativa que contém uma associação correta.
A senha bancária da conta corrente de uma grande em-
presa é formada por cinco algarismos, e ficou estabeleci-
do que ela fosse modificada semanalmente.
Para tanto,os responsáveis pela movimentação financeira da em-
presa fixaram um algoritmo, que corresponde à soma dos
dois últimos elementos de uma sequência numérica, com
nove elementos, que seria modificada a cada semana:
quando essa soma tivesse menos de cinco algarismos,
ela seria completada com zero(s), no final, até atingir os
cinco algarismos; se tivesse mais de cinco algarismos,
seria(m) excluído(s) o(s) último(s) algarismo(s).
Em determinada semana, a sequência numérica fixada
tinha os seguintes sete primeiros elementos:
1, 2, 7, 14, 31, 62 e 127
Naquela semana, a senha bancária foi
Certo vírus foi disseminado pela internet e, inicialmente,
foram identificados cinco mil computadores infectados.
A estimativa dos profissionais capacitados para resolver
o problema é a de que o número y(x) de computadores
infectados cresça até um valor máximo m e, a partir daí,
ele comesse a cair, onde y(x) representa o número de
computadores infectados após x dias do início da disse-
minação, com y(0) representando o número de computa-
dores infectados inicialmente. Supondo-se que a razão
entre a diferença y(x) – m e o quadrado da diferença
x – 4 permaneça constante, e sabendo-se que 2 dias
após o início da disseminação o número de computado-
res infectados era 9 800, o valor máximo de computado-
res infectados, ou seja, o número m, é igual a
Alberto, Carlos, Douglas e Edgar têm 35, 38, 40 e 41
anos, não necessariamente nessa ordem. Cada um deles
trabalha com um tipo de veículo, sendo eles caminhão,
carro, motocicleta e ônibus, em municípios distintos, sendo
Campinas, Limeira, Marília e Santos, não necessariamente
nas ordens apresentadas. Sabe-se que o de maior
idade trabalha com carro e seu local de trabalho não é
Limeira e, tampouco, Marília; Alberto tem menos idade
que Douglas, trabalha em Campinas, não com ônibus, e
o mais novo deles trabalha em Limeira, com motocicleta;
Edgar não trabalha com ônibus e é mais velho que
Alberto e que Douglas. A alternativa que apresenta uma
associação correta dessas pessoas é:
Considere uma das sequências formadas pelas letras do conjunto {A, B, C, D, E}.
Sabe-se que nessa sequência:
- B vem depois do D;
- C vem antes do A;
- E vem depois do D;
- E vem antes do A;
- C vem depois do B.
Com base nessas informações, é possível garantir que, nessa sequência, a letra A ocupa a
Qual é o valor de n na sequência (10,1,9), (9,2,49), (8,3,125), (7,4,n)?
Considere duas sequências, A e B, cada uma criada com o próprio padrão lógico. Na sequência A, o primeiro termo apresentado é o 1, e o último termo é o 97.
A = (1, 2, 4, 7, 9, 10, 12, 15, 17, 18, 20, 23, 25, ..., 97)
Na sequência B, o primeiro termo apresentado é o 100, e o último termo é o 4.
B = (100, 97, 95, 94, 92, 89, 87, 86, 84, 81, 79, 78, 76, ..., 4)
Observe os exemplos a seguir. A diferença, em valor absoluto, entre os números do par formado pelos primeiros termos de cada sequência, o 1 e o 100, é igual a 99 (100 – 1). A diferença, em valor absoluto, entre os números do par formado pelos sétimos termos de cada sequência, o 12 e o 87, é igual a 75 (87 – 12).
O par de termos de cada sequência que, pareados conforme os exemplos anteriores, apresenta a menor diferença absoluta entre seus termos está localizado na posição
A partida decisiva Maiorais x Geniais envolve uma grande incógnita. O goleiro Pegatudo, dos Geniais, está machucado, e a probabilidade de sua presença em campo é de 60%. Das últimas 10 partidas entre as equipes com Pegatudo no gol, os Geniais ganharam 7 e perderam 3. Porém, nas últimas 4 vezes em que Pegatudo esteve ausente, os Maiorais venceram 3 e só perderam 1.
Usando esses dados, a probabilidade que os Geniais saiam vencedores do confronto é estimada em
A Mega-Sena é um jogo de apostas no qual são sorteadas 6 dentre 60 bolas numeradas de 1 a 60. Cecília fez uma aposta, escolhendo os números 1, 2, 3, 4, 5 e 6. Cecília está acompanhando o sorteio e viu que as três primeiras bolas sorteadas foram as de número 1, 2 e 3.
A chance de Cecília acertar os seis números e ganhar na Mega-Sena é agora de uma em
Um professor de práticas esportivas decidiu anotar a altura e o peso de seus alunos, montando a seguinte tabela.
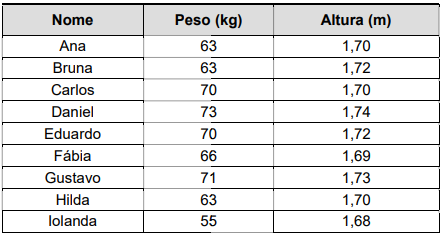
Com base nesses dados, e considerando corretamente os conceitos estatísticos de média, moda e mediana, assinale a alternativa correta.
Considerando o símbolo → representando a implicação. Considerando, também, três fórmulas bem formadas quaisquer, da lógica proposicional α, β e θ, sendo θ = α→β, em qual circunstância θ é uma contradição?
Tendo o texto acima como referência inicial, julgue os itens de 33 a 35.
O número de anagramas da palavra NIEMEYER que possuem as vogais e consoantes alternadas é igual a 576.
. Huguinho, Zezinho e Luisinho haviam combinado de seencontrar em frente à prefeitura da cidade às 16 horas paraandar de bicicleta no parque. Zezinho, que chegou 10 minutos antes do horário marcado, teve que esperar por 25 minutosaté a chegada de Huguinho. Huguinho, por sua vez, chegou5 minutos depois de Luisinho. Sendo assim, pode-se concluir que:
