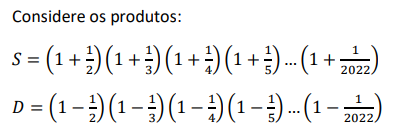De um grupo de 1000 soldados, uma parte foi dividida em grupos de 15 soldados e o restante foi dividido em 5 grupos de 17 soldados.
O número de grupos de 15 soldados é
Um campeonato de judô contou com seis atletas. Cada atleta participante lutou exatamente uma vez contra cada um de seus oponentes. Nesse campeonato, uma vitória vale 2 pontos, um empate vale 1 ponto e uma derrota vale 0. Ao final do campeonato, um dos atletas somou 8 pontos, outro somou 6 pontos, e os quatro restantes obtiveram o mesmo número de pontos cada um.
O número de pontos de cada um dos quatro atletas restantes é
A sequência mista 4, 8, 7, 5, 10, 9, 13, 6, 16, 10, 19, 7, … contém os elementos de duas sequências, sendo uma delas formada pelos elementos que ocupam as posições ímpares e a outra pelos elementos das posições pares.
Nessa sequência mista, subtraindo seu 100º elemento de seu 99º elemento, obtemos
Uma dívida de R$ 81.400,00 foi negociada para ser paga em duas parcelas, a primeira no momento da assinatura do acordo e a segunda 30 dias depois. Sobre a segunda parcela incidirão juros de 3,5% sobre o saldo devedor.
Após decidido o valor a ser pago no momento da assinatura do acordo, constatou-se que as parcelas seriam iguais, valores esses iguais a
Um bolo pesa 1600 gramas. Ele foi cortado em 5 pedaços, sendo um deles mais pesado e os outros quatro com o mesmo peso.
O pedaço maior tem o mesmo peso dos quatro pedaços menores juntos. O peso do pedaço maior, em gramas, é
No retângulo ABCD da figura abaixo, AB = 600 m e BC = 400 m. O retângulo está em um plano horizontal dividido em quadrados
iguais. Pedro e Mário estão no ponto A e pretendem atingir o ponto P, cada um por um caminho, sobre as linhas destacadas do
desenho. Pedro inicia seu percurso na direção do ponto D e Mário inicia seu percurso na direção do ponto B. Ambos chegam ao ponto P.
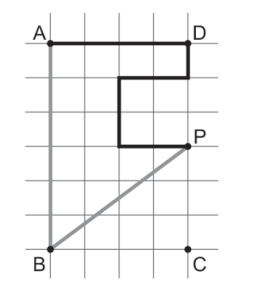
É correto afirmar que
Com 64 cubinhos brancos, de dimensões 1 × 1 × 1, montou-se um cubo de dimensões 4 × 4 × 4. As faces do cubo grande foram pintadas de azul. O número de cubinhos que ficaram sem nenhuma face pintada de azul é
Julgue o item a seguir, com base em conhecimentos da matemática.
Considere que dois lagartos (A e B) sejam de uma espécie que se alimenta apenas de dois tipos de insetos: mosquitos e mariposas. Considere, ainda, que, em certo dia, o lagarto A tenha comido 8 mosquitos e 4 mariposas, que correspondem a 236 calorias, enquanto o lagarto B tenha comido 6 mosquitos e 2 mariposas, que correspondem a 160 calorias. A partir dessas informações, conclui-se que uma mariposa contém 21 calorias.
Em uma fila com 12 cadeiras, três delas foram ocupadas aleatoriamente. A cadeira em que Valter deverá se sentar será sorteada entre as cadeiras que estão vazias.
A probabilidade de que Valter não se sente ao lado de nenhuma pessoa já sentada é, no mínimo:

Dos números apresentados abaixo, o único que pode ser escrito como a soma de 4 números inteiros consecutivos é
Três amigos, Ângela, Beatriz e Caio decidiram constituir uma empresa em sociedade. Ângela investiu R$ 3.000,00. Beatriz, R$ 2.700,00 e Caio, R$ 1.800,00. Ao final de um ano, a empresa obteve um lucro de R$ 3.000,00 que deve ser dividido em partes proporcionais aos valores investidos por cada sócio. Com base nessas informações, podemos dizer que:
Um tigre avista um javali a 1km de distância e sai, em linha reta, em seu encalço. Nesse instante, o javali foge na direção contrária
à do tigre. O tigre corre a 30m/s, e o javali tenta escapar a uma velocidade de 10m/s. A distância percorrida pelo javali até ser alcançado pelo tigre é igual a
Tendo em vista essas informações, as dimensões, em metros, três canteiros medidos por cada uma dessas três pessoas. Serão, respectivamente,