Quando os amigos Marcelo, Nina, Otávio, Pietra e Quincas saem juntos, quem usa brinco sempre mente, e quem não usa sempre fala a verdade. Observe o seguinte diálogo que os amigos tiveram em um passeio que fizeram juntos:
Marcelo: Nina está de brinco ou Otávio não está de brinco.
Nina: Marcelo não está de brinco e Quincas está de brinco.
Otávio: Pietra está de brinco.
Quincas: ou Pietra está de brinco ou Nina está de brinco.
Nesse passeio, em relação a estar sem ou com brinco, temos, respectivamente, que Marcelo, Nina, Otávio, Pietra e Quincas estão
As interpretações mais comuns sobre Resolução de Problemas são:
1) como uma meta;
2) como um processo;
3) como uma habilidade básica;
4) como metodologia para o ensino de matemática.
Diante do exposto, analise as assertivas a seguir e assinale a alternativa que aponta a(s) correta(s).
I. Como meta, a Resolução de Problemas visa apresentar aos alunos problemas diversificados, que exijam raciocínio e não conhecimentos matemáticos elencados nos currículos escolares, pois o importante é a elaboração de pensamentos e não a utilização de conceitos previamente ensinados.
II. Como processo, são valorizados os métodos, os procedimentos e as estratégias que os alunos usam na resolução das situações propostas e, assim, surgem os tipos de problemas, os tipos de estratégias de resolução e os esquemas de passos a serem seguidos para melhor resolver problemas.
III. Como habilidade, a Resolução de Problemas deve ser entendida como uma competência mínima para que o indivíduo possa inserir-se no mundo do conhecimento e do trabalho e deve levar em consideração o conteúdo específico, os diversos tipos de problemas e os métodos de resolução de problemas para que se alcance a aprendizagem matemática.
Em um esquema de vacinação, observou-se que todos os professores de uma escola foram vacinados contra três tipos de doença: A, B e C. Sabe-se que nenhum professor foi vacinado contra as três doenças, 10 foram vacinados contra as doenças A e B, 10 foram vacinados contra as doenças B e C e nenhum foi vacinado contra as doenças A e C. Sabe-se, ainda, que: a quantidade de professores que foram vacinados contra a doença B é o dobro da quantidade de professores que foram vacinados contra a doença A; a quantidade de professores que foram vacinados contra a doença C é o triplo da quantidade de professores que foram vacinados contra a doença A; a diferença entre a quantidade de professores que foram vacinados contra a doença C e a quantidade de professores que foram vacinados contra a doença B é 20. Nessas condições, assinale a alternativa correta.
A Loja Tesla, na promoção “Pula pula”, oferece uma televisão por R$ 1.050,00, com pagamento integral desse valor para dois meses depois do dia da compra. Um cliente propõe pagar à vista, o gerente calcula o desconto racional, no regime de juros simples, e cobra o valor atual de R$ 840,00. A taxa mensal de juros calculada neste caso foi de
O quadro a seguir apresenta o percentual de votos que os candidatos A, B e C obtiveram na eleição para diretor de uma escola.
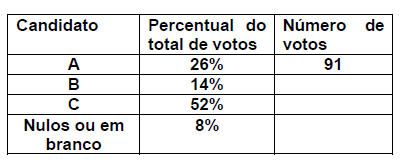
Nessas condições, o número de votos nulos ou em branco foi de
eja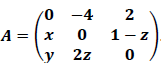 
. Sabendo que
Julgue o item a seguir, relativos a triângulos retângulos, funções trigonométricas e geometria analítica.
Se um triângulo retângulo possui lados cujos comprimentos são números inteiros e um dos catetos mede 14 cm, então o outro cateto mede mais de 40 cm.
Leonor tem uma caixa com 600 botões. Nessa caixa, 2/5 dos botões são brancos e 150 botões são amarelos. Dos restantes, 1/3 são vermelhos e 2/3 são azuis. Leonor vendeu 5% dos botões brancos, 10% dos amarelos e 20% dos vermelhos. Após a venda, o número de botões que restou na caixa foi
A figura abaixo mostra o gráfico da função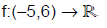 
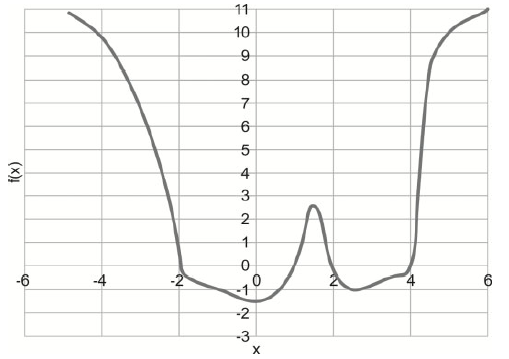
número de soluções da equação f(f(x)) = 0 é
Considere uma parte de um gráfico de uma parábola formada pelos pares coordenados (x,y) que satisfazem a equação y = ax2 + bx + c.
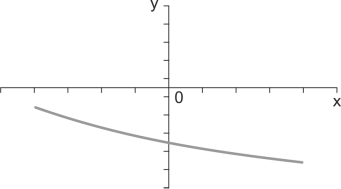
É correto afirmar que:
Julgue o próximo item, relativo a sequência de número real.
Se (an) for uma sequência de números reais, de forma que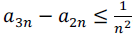 
, então a sequência (an) converge.
João vai e volta da escola a pé ou de ônibus. O tempo de ida e volta é o mesmo para a mesma escolha de transporte e diretamente proporcional à distância percorrida. Quando João vai de ônibus e volta a pé, demora 3 horas. Quando vai e volta de ônibus demora 1 hora. Se ele for para a escola a pé e voltar metade da distância a pé, o restante de ônibus, demorará
As amigas Ana, Bruna, Carla e Denise vão a uma festa e cada uma tem um vestido. Como querem usar um vestido diferente, decidiram que cada uma irá usar o vestido de uma das outras. O número de maneiras distintas de fazerem isso é igual a
Um número inteiro positivo, N, somado ao seu dobro é igual à sua metade mais 10. O valor de N é
