O custo de uma empresa, para produzir x unidades de um certo produto, é dado pela lei C(x) = −x² + 190x, e a receita
arrecadada com a venda desses produtos é dada por R(x) = 2x² − 500x.
Sabendo-se que o lucro é L(x) = R(x) − C(x), o número mínimo de peças que essa empresa precisa fabricar para que haja
lucro é
A sequência representa uma P.A. crescente e a sequência (x − 1, 8, y) representa uma P.G. crescente. Está correto afirmar que x + y vale
A reta r tem equação x + 3y − 6 = 0. Assim, a área da região determinada pela intersecção da reta r com os eixos coordenados é
Em um órgão público, 40 relatórios de prestação de contas
que apresentaram erro serão novamente analisados e, para que esse
trabalho seja executado mais eficientemente, esses relatórios foram
separados em dois grupos (A e B), cada um com 20 relatórios. Em
cada grupo, os relatórios foram classificados, de acordo com o erro
apresentado, em EM = relatório com erro de natureza média;
EG = relatório com erro de natureza grave; ou EGS = relatório com
erro de natureza gravíssima. Escolhendo-se, aleatoriamente, um
relatório do grupo A, sabe-se que as probabilidades de ele ser
classificado como EM, EG ou EGS são, respectivamente:
PA(EM) = 0,5; PA(EG) = 0,3; PA(EGS) = 0,2. No caso de relatório
do grupo B, as probabilidades são: PB(EM) = 0,1; PB(EG) = 0,6;
PB(EGS) = 0,3.
A probabilidade de se escolher, aleatoriamente, três relatórios,
sendo dois do grupo A e um do grupo B, todos classificados
como EGS, é expressa por (4/20) × (3/19) × (6/20).
O número de miniaturas de carros da coleção de Rogério aumenta, a cada mês, de acordo com uma progressão aritmética. No sexto mês, a coleção tinha 40 miniaturas, no oitavo tinha 52. No vigésimo mês, a coleção terá a seguinte quantidade de miniaturas:
Uma carta náutica foi planejada na forma de um sistema de coordenadas cartesianas em que cada unidade equivale a 100 milhas. Assim, se o sistema mostra que uma embarcação se deslocou, em linha reta, do ponto (0,0) ao ponto (2,0) isso significa que ela percorreu 200 milhas na direção leste.
Se a carta indica que um determinado barco se deslocou em linha reta do ponto (2,1) até o ponto (2,3) e, em seguida, ainda em linha reta, do ponto (2,3) até o ponto (6,3), concluímos que o barco percorreu, na realidade, a seguinte distância, em milhas:
Ao mostrar um projeto para um amigo, um arquiteto diz: “Este arco terá cinco pi sobre seis radianos”. O amigo entendeu que o arquiteto se referiu a ( 5 ) / 6 rad, converteu para graus e obteve:
Avalie as afirmativas a seguir em relação à função real
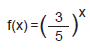
I: f(0) = 1
II: f é crescente
III: A imagem de f é o intervalo ( 0 ; )
Está correto o que se afirma em:
Um anagrama de uma palavra é uma reordenação qualquer de suas letras. Por exemplo, ASAC é um anagrama de CASA, CAAS é outro anagrama de CASA. A palavra MILITAR tem a seguinte quantidade de anagramas:
Considere o sistema abaixo:
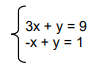
O par ordenado que soluciona este sistema é
Atenção: Para resolver às questões de números 52 e 53, considere os dados abaixo:
A empresa de aviação T tem 4 balcões de atendimento ao público: A, B, C e D. Sabe-se que, num determinado dia, os balcões A e B atenderam, cada um, a 20%; C e D atenderam, cada um, a 30% do público que procurou atendimento em T. Sabe-se ainda que A, B, C e D atenderam, respectivamente, 5%, 15%, 10% e 20% de pessoas com atendimento prioritário (idosos, deficientes, gestantes ou mães com crianças no colo, etc).
Selecionando-se ao acaso e com reposição cinco pessoas atendidas no balcão D, nesse mesmo dia, a probabilidade de exatamente duas terem sido do grupo de atendimento prioritário é de
Um dado é viciado de tal modo que a probabilidade de ocorrer face par é duas vezes mais provável do que ocorrer face ímpar. O dado é lançado duas vezes independentemente. Considere os seguintes eventos:
A = a soma dos pontos das faces é 6;
B = o número da face do primeiro dado é menor do que 3.
Nessas condições, a probabilidade de A, sabendo que ocorreu B, é
Se f(x) = | x – 3 | – | 2 – x | então f(– 2) é igual a:
O determinante da matriz
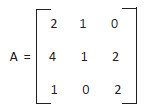
é igual a:
Se f(x) = 3 – 2x, x real, então f(–5) é igual a:

