Calcule o primeiro termo de uma progressão aritmética, sabendo que a soma do terceiro termo com o nono termo é igual a 20 e, que a soma do décimo quinto termo com o trigésimo segundo termo é igual a 90.
Calcule a medida do lado de um triângulo equilátero ABC, sendoA(5, -3) e B(-3, 3).
Dentro de um saco há 24 balas, todas indistinguíveis, a não ser por seus sabores: 6 são de morango, 8 de caramelo e 10 de hortelã. Uma pessoa coloca a mão dentro do saco e pega n balas.
Para que essa pessoa tenha certeza de que pegou pelo menos duas balas de hortelã, o menor valor de n deverá ser
Numa empresa trabalham 80 funcionários, dos quais 20 são mulheres. Se forem contratadas mais 10 mulheres, sem que nenhum funcionário antigo seja demitido, o percentual de mulheres nessa empresa passará a ser, aproximadamente, de
Acerca de questões atinentes a matemática financeira, julgue os itens subsecutivos.
Considerando-se que a inflação nos últimos três meses tenha sido de 1%, 2% e 3%, é correto afirmar que a inflação média no período foi de 2%.
Determine o valor de m que é solução da equação abaixo.
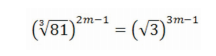
Determine a altura de um poste, cuja sombra, no momento em que os raios solares formam um ângulo ß = 3/5. Considere senß = 3/5.
Calcule o valor do produto abaixo.
10% . 20% . 30% . 40%
Determine o valor do ângulo que é igual a 2/3 do seu suplemento.
Considerando G o baricentro de um triângulo MPQ e, sabendo que a mediana relativa a PQ, mede 12 cm, determine a distância GM.
Sejam M e N os pontos médios de dois lados paralelos de um hexágono regular. Se MN = 2√3, determine a medida do lado deste hexágono regular.
Maria e João arremessam, cada um, uma moeda, perfeita. Sabendo que Maria arremessou duas vezes sua moeda e, João, arremessou uma só vez a sua, determine a probabilidade de Maria conseguir a mesma quantidade de caras que João.
Determine a equação da reta mediatriz do segmento AB, sendo A (1, 4) e B (-2, -2).
Seja M (1, -5) o ponto médio do segmento AB, onde A (-4, 0). Calcule a soma das coordenadas do ponto B.
Observe as figuras a seguir:
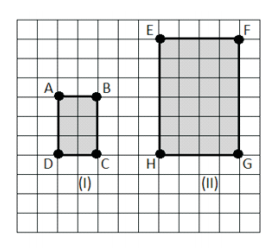
Em relação às figuras ( I ) e ( II ), pode-se afirmar que:

