O número de computadores de mesa (desktops) de uma empresa é igual a quatro vezes o número de computadores portáteis (laptops). O número de computadores portáteis é igual a dez vezes o número de aparelhos de fax da empresa. De acordo com esses dados, o número de aparelhos de fax dessa empresa corresponde à
O conselho diretor de uma empresa teve os mesmos 5 membros
desde o ano 2012. Na última reunião deste ano de 2015 o
membro mais velho, que tinha 58 anos, foi substituído por um
mais jovem, mas a média de idade dos membros do conselho
ficou igual à média das idades na mesma época de 2012
Na reunião de 2015, a idade do novo membro do conselho era de:
No primeiro turno do campeonato piauiense de futebol 6 times participam, mas somente 4 chegam às semifinais. O número de possibilidades diferentes para o conjunto dos 4 times que estarão nas semifinais é:
A figura abaixo mostra a planta de um salão. Os ângulos A, B, C, D
e E são retos e as medidas assinaladas estão em metros.
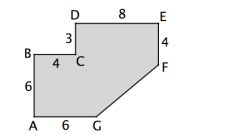
A área desse salão em m²
é:
Para estimar o valor da diferença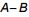 
, Tales diminuiu o valor
de A de um pequeno valor positivo e aumentou o valor de B do
mesmo pequeno valor, subtraindo então os resultados
encontrados.
A estimativa obtida por Tales foi obrigatoriamente:
A figura a seguir mostra um salão poligonal ABCDEF, onde os
ângulos internos nos vértices A, B, C, D e F são retos e as medidas
indicadas estão em metros.
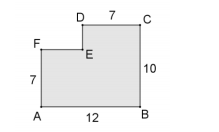
O perímetro e a área desse salão são, respectivamente:
Pedro caminha qualquer distância em um quarto do tempo que seu
filho Junior leva para caminhar a mesma distância.
Pedro e Junior partem simultaneamente do ponto O, em direções
opostas, caminhando na pista retangular mostrada a seguir, na
qual O e C são, respectivamente, os pontos médios de EA e DB. As
dimensões da pista retangular, em metros, são EA = 13 e AB = 7.
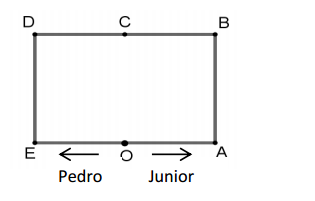
Quando Pedro e Junior se encontrarem pela primeira vez, eles
estarão mais perto do ponto:
Ao longo de uma estrada aparecem as cidades A, B, C e D, nessa ordem. Sabe-se que a distância entre as cidades A e C é de 30km, a distância entre as cidades B e D é de 43km e que a distância entre as cidades A e D é de 55km. A distância entre as cidades B e C, em quilômetros, é igual a:
João coordena as 5 pessoas da equipe de manutenção de uma empresa e deve designar, para cada dia, as pessoas para as seguintes funções: • uma pessoa da equipe para abrir o prédio da empresa e fiscalizar o trabalho geral; • duas pessoas da equipe para o trabalho no turno da manhã, deixando as outras duas para o turno da tarde. O número de maneiras diferentes pelas quais João poderá organizar essa escala de trabalho é:
Francisco vendeu seu carro e, do valor recebido, usou a quarta parte para pagar dívidas, ficando então com R$ 21.600,00. Francisco vendeu seu carro por:
Considere a afirmação: “Mato a cobra e mostro o pau” A negação lógica dessa afirmação é:
Em um saco há 3 bolas brancas, 3 bolas amarelas e 3 bolas vermelhas. Duas delas são retiradas ao acaso. A probabilidade de que essas bolas sejam de cores diferentes é:
A figura abaixo mostra a planta de um salão. Os ângulos A, B, C, D
e E são retos e as medidas assinaladas estão em metros.
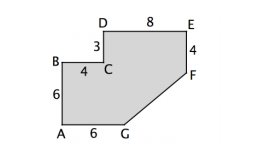
A área desse salão em m2
é:
Pedro caminha qualquer distância em um quarto do tempo que seu
filho Junior leva para caminhar a mesma distância.
Pedro e Junior partem simultaneamente do ponto O, em direções
opostas, caminhando na pista retangular mostrada a seguir, na
qual O e C são, respectivamente, os pontos médios de EA e DB. As
dimensões da pista retangular, em metros, são EA = 13 e AB = 7.
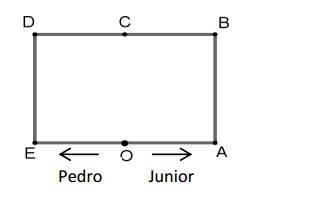
Quando Pedro e Junior se encontrarem pela primeira vez, eles
estarão mais perto do ponto:
Como decoração para o Natal, 39 pontos de iluminação foram instalados em toda a extensão de uma rua comercial. Esses pontos foram divididos entre os dois lados da rua, sendo que o lado de numeração par recebeu 3 pontos a mais que o lado de numeração ímpar, e posicionados de modo que ambos os lados tivessem um ponto colocado exatamente no início e outro ponto colocado exatamente no final da rua. Sabendo que no lado par a distância entre dois pontos de iluminação consecutivos foi sempre igual a 12,5 m, é correto afirmar que a extensão dessa rua é igual, em metros, a
