A área total de um paralelepípedo com dimensões de 6 cm, 8 cm, e 10 cm e o volume deste mesmo paralelepípedo são, respectivamente:
João tinha uma quantia, gastou 33% e ainda ficou com R$ 402,00. Qual o valor que João tinha inicialmente?
Lavínia comprou um carro no valor de R$ 29.760,00, dividido em 48 prestações iguais (sem juros). Ao pagar a 30º prestação, recebeu de presente de seu avô, o restante do dinheiro para a quitação do veículo. Quanto Lavínia recebeu?
A coleta seletiva da cidade de Sarzedo recolhe semanalmente 9.570kg de resíduos recicláveis. Portanto, em três meses terá recolhido:
(Considerar um mês com 4 semanas)
A razão entre a soma e o produto das raízes da equação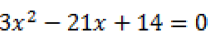 
é:
Observe as pirâmides mágicas a seguir:
De acordo com as pirâmides mágicas anteriores, o valor da soma do dobro do valor de X com a centésima parte do valor de Y, é:
Andréa, Anderson e Osvaldo fizeram uma prova de concurso contendo 20 questões de matemática, com as seguintes regras:
- Cada resposta certa o candidato ganha cinco pontos;
- Cada questão deixada em branco não será pontuada;
- Cada resposta errada o candidato perde dois pontos.
Na tabela a seguir tem-se o desempenho dos três candidatos:
Depois de analisados os dados anteriores e organizado as notas de cada um dos candidatos em ordem crescente, teremos seguinte classificação:
Um automóvel popular consome 1 litro de combustível para percorrer 12km. Assinale a alternativa que apresenta CORRETAMENTE a quantidade de litros de combustível serão gastos para um trajeto de 156km.
Seja a equação: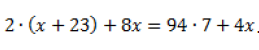 
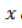
. Para que a sentença seja verdadeira o valor de 
deve ser igual a:
Em relação aos 31 dias de um mês, Fernando, Geraldo e Hélio folgaram, respectivamente, nos dias que são “múltiplos de 6”, “divisores de 12” e “múltiplos de 3 e divisores de 30”. Nesse mês, os três trabalharam juntos em um total de
Uma pessoa inicia uma prova às 8h 12 min e conclui às 11h 37 min. Sabendo que do tempo gasto ela utilizou 40% para responder as questões de conhecimentos gerais e 60% para responder as questões de conhecimentos específicos podemos afirmar que:
Um determinado reservatório de água tem a capacidade de 500.000 litros de água. Para abastecê-la com caminhões pipa com capacidade de 10m3, quantos caminhões serão necessários?
A padaria Pão Doce faz compras semanais de farinha. Em cada compra é feito a encomenda de 50Kg do produto. Mas, devido as festas de fim de ano, foi preciso aumentar o volume de compra para 125Kg. Qual a porcentagem que demonstra o aumento ocorrido entre a primeira e a segunda compra?
Selecione a opção que mostra uma função decrescente.
Paola mora em uma casa em que o telhado tem o formato de um triângulo isósceles. Sabendo que o lado deste triângulo mede 25 metros e sua altura sendo 15 metros. Qual o valor da base?
