Seja a P.G. (24, 36, 54, ...). Ao somar o 5º e o 6º termos dessa P.G. tem-se
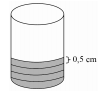
Um cilindro circular reto de 5 cm de raio da base e de 10 cm de altura terá toda a sua superfície lateral revestida por uma fita de 0,5 cm de largura, como mostra a figura. Considerando π = 3,14 e que não haverá sobreposição de fita, será necessário uma quantidade mínima de ______ m de fita para realizar a tarefa.
Seja r a reta determinada por A (3, 5) e B (6, −1). O ponto de abscissa 8 pertencente à r possui ordenada igual a
Ainda a partir das informações do texto 1A3-II, conclui-se que a produção total de batatas da fazenda Alfa, colhida desde o ano de 2001 até o ano de 2020, foi igual a
Considere que, quando Carlos, agente de pesquisas por telefone, realiza uma chamada telefônica, a chance de que a sua chamada não seja atendida seja de 20% e que, se a chamada for atendida, a chance de que ele obtenha respostas verdadeiras seja de 60%. Nessa situação, a probabilidade de Carlos obter respostas verdadeiras em uma dada chamada telefônica é igual a
A roda do caminhão do Seu João dá 2.750 voltas em 120 segundos. Se a velocidade permanecer constante, quantas voltas essa mesma roda dará em 300 segundos?
Quantos números de dois algarismos distintos podem ser formados com os números: 0,1,2,3,4,5,6,7,8,9?
A viatura V emite um sinal de emergência para a central de rádio que está localizada a uma distância de 32 km a oeste e 8 km ao sul dessa viatura. O pedido de emergência à central consiste em localizar a viatura W para auxiliar no atendimento a determinada ocorrência. A central consegue transmitir sinais em todas as direções até a distância máxima de 50 km. A central consegue descobrir que a viatura W está a uma distância de 25 km da central, a 7 km ao sul da central, determinando assim dois pontos possíveis onde possa estar a viatura W.
Com base nessas informações e sabendo-se que a distância entre as viaturas V e W é a mínima entre as duas distâncias possíveis — determinadas com base nos dois pontos em que a viatura W pode estar localizada —, é correto afirmar que a distância entre elas, em quilômetros, é igual a
Em um pelotão do corpo de bombeiros com 30 soldados, apenas 12 sabem conduzir motocicletas, apenas 5 sabem pilotar helicópteros e apenas 3 sabem pilotar helicópteros e conduzir motocicletas. Nessa situação, o número de soldados nesse pelotão que não sabe conduzir motocicleta nem sabe pilotar helicópteros é igual a
Na primeira semana de uma estação seca, o corpo de bombeiros usou 3 horas do primeiro dia para o combate a incêndios. Naquela semana, a quantidade diária de horas usadas para o combate a incêndios aumentou em progressão aritmética com razão igual a 20 minutos.
Nessa situação, a quantidade de tempo usada para o combate a incêndios nos 7 dias daquela semana foi
Considere que, t minutos após o início da utilização da água de um tanque, a porcentagem de água no tanque seja igual a p(t) = 110 – 100,025t + 1. Nesse caso, se o tanque deve ser reabastecido quando a porcentagem de água no tanque chega a 10%, então o tempo de utilização do tanque até que seja necessário reabastecê-lo é igual a
Um irrigador distribui água numa região circular, de raio 13,5 m. Devido a um defeito, esse irrigador precisou ser trocado por outro, que passou a irrigar uma região circular de raio 18 m. Assinale a alternativa que apresenta a área da parte cinza, indicada na figura abaixo, que corresponde à região que passou a ser coberta pelo segundo irrigador, além daquela coberta pelo primeiro.
O Sgt. PM J.B. tira serviço de 4 em 4 dias, e o cabo PM B.J. tira serviço de 5 em 5 dias. Se os dois estavam de serviço juntos na mesma guarnição no dia 5 de dezembro, em qual dia do mês de janeiro estarão de serviço juntos novamente?
Em uma farmácia, o preço de uma caixa de vitamina C é igual à multiplicação do número complexo A pelo seu conjugado B, onde ai. Um cliente foi a essa farmácia e deu duas notas de R$ 100,00 para comprar uma caixa de vitamina C. Com base nessa situação hipotética, assinale a alternativa que apresenta o valor do troco que deverá ser entregue ao cliente.
Abaixo temos 3 proposições:
I) √ x2=x , para todo x real.
II) |−x|=x , para todo x real.
III) para todo x real.
Analisando as proposições acima, podemos afirmar que

