Priscila, que sempre foi uma menina muito curiosa, decidiu, durante uma festa de família, perguntar a idade de todos à sua volta. Seu Primo Lucas tem 8 anos, sua tia Ana tem 27, o tio Bento tem 33 anos, seu outro tio David tem 45 anos e sua irmã Beatriz tem 12 anos. Qual o Média das idades da família de Priscila?
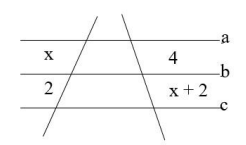
Utilizando a Teorema de Tales, encontre os valores de x, sabendo que as retas a, b e c são paralelas.
Nas compras acima de R$ 100,00, o cliente ganha um cupom, para o sorteio de uma TV. O sorteio será aberto ao público, com bolinhas numeradas de 0 a 9. Quantas são as possibilidades de sorteio visto que o número da sorte é uma sequência de quatro números?
Sobre os triângulos. Marque a opção incorreta.
Qual é o resultado de 3 + 6 . 5 – 8 : 4 ?
Um pintor costuma dissolver cada 2 latas de tinta concentrada em 3 latas de água. Para que a tinta tenha a mesma concentração, esse pintor precisará misturar 12 latas de água com quantas latas de tinta?
Em uma empresa com 120 funcionários, 42 recebem vale-transporte e 95 recebem vale-refeição. Sabendo que todos os funcionários da empresa recebem ao menos um desses dois benefícios, o total de funcionários que recebem ambos os benefícios é igual a
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
Se 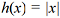
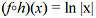
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A diferença entre os percentuais de água contida na represa em 31/12/2017 e 1.º/1/2017 é superior a 20%.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
Em 2017, a quantidade de água acumulada no reservatório ficou acima de 51% de sua capacidade máxima em dias de exatamente 4 meses.
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
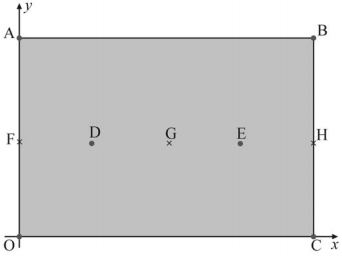
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
A reta que contém os pontos B e E intercepta o eixo Ox no ponto de abscissa x = 300.
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.

A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Considere que uma pessoa esteja em ponto P da região retangular de modo que o ângulo OPA seja igual a 90°. Nesse caso, se o cosseno do ângulo AOP for igual a 0,3, essa pessoa estará a mais de 200 m da origem O.
A respeito dos números complexos, julgue o item a seguir.
Se n for um número par e se p for um número real diferente de zero, então o polinômio zn + p = 0 tem, necessariamente, duas raízes reais distintas.
A respeito dos números complexos, julgue o item a seguir.
Se n > 1 for um número inteiro e se ω ≠ 1 for uma raiz n-ésima da unidade (isto é, ωn = 1), então 1 + ω +...+ ωn-1 = 0.
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se 0 é a matriz nula n × n, se I é a matriz identidade n × n, e se P é uma matriz n × n tal que P2 + 2P + I = 0, então P é inversível.

